Planeación agregada mediante programación lineal

Recordemos que la planeación agregada es un proceso utilizado para determinar una estrategia de forma anticipada que permita satisfacer los requerimientos (demanda) del sistema, al mismo tiempo que busca optimizar los recursos del mismo; cuyo desarrollo se lleva a cabo en el corto y mediano plazo.

Variables y consideraciones

A la hora de elaborar un plan agregado se debe tener en cuenta que existen una serie de consideraciones que rigen la estrategia, ya sea por el horizonte de tiempo, por el criterio de las decisiones o por las restricciones que delimitan el sistema.

A continuación detallaremos estas consideraciones:

Horizonte de tiempo

Básicamente, la planeación agregada considera un horizonte de tiempo de corto y medio plazo, es decir que suele manejar un periodo entre 6 y 18 meses de planificación.

Criterios de decisión

El principal objetivo de la planeación agregada es aumentar la productividad, de manera que debe acercar a la organización a su meta económica. En este orden de ideas, la búsqueda de la maximización del beneficio se alinea con los objetivos del plan agregado, entendiéndose como la diferencia entre los ingresos y los gastos operativos, por ende es válido considerar la minimización de los costos totales (mientras no se afecten los ingresos) como criterio de decisión de la planeación agregada.

Teniendo en cuenta lo anterior, es necesario evaluar con espíritu crítico y perspectiva sistémica, todas las relaciones entre los recursos disponibles para llevar a cabo el plan y sus implicaciones en los costos totales. De manera que pueden identificarse los costos asociados a los siguientes factores:

Restricciones

Todos los sistemas objetos de planeación agregada se encuentran sujetos a restricciones y de diversos tipos, tales como:

Modelos de programación lineal en planeación agregada

Existen diversos métodos empleados en la creación de un plan agregado, entre los que se destacan la programación lineal, reglas de decisión por búsqueda, programación por objetivos, programación dinámica, o métodos heurísticos (ensayo y error).

La programación lineal por sus características innatas de modelación libre, se constituye como una herramienta poderosa de resolución de planes agregados, de manera que puede considerar tantas restricciones como la realidad del sistema lo presenten, al mismo tiempo que se enfoca en soluciones óptimas, a diferencia de los métodos heurísticos de comparación de alternativas.

A continuación, se detallará un modelo de programación lineal mixta propuesto por el autor, que considerará la mayor parte de los criterios de decisión contemplados en los métodos heurísticos de comparación de alternativas, en búsqueda de una solución óptima.

Modelo de programación lineal mixta aplicado a Planeación Agregada

En el modelo propuesto las decisiones se toman de acuerdo con una fuerza de trabajo flexible considerando tiempo extraordinario de trabajo y una tasa de producción que contempla un factor de eficiencia reducida para operarios nuevos en el periodo de contratación, simulando el impacto de la curva de aprendizaje.

Los costos que afectan la función objetivo se expresan en «costos por unidades agregadas» y «costos por operario», e incluye los componentes de:

Además, los costos asociados al tiempo normal y extraordinario relacionados con los operarios nuevos también contemplan el factor de eficiencia reducida por periodo.

Datos de entrada requeridos

El modelo que hemos preparado requiere de los siguientes datos de entrada:

m = Número de periodos del plan

días = Número de días de cada periodo del plan

requerimientos = Los requerimientos estimados de cada periodo del plan (unidades)

Jornada laboral = Jornada laboral en términos de horas / día

Tiempo unitario = Tiempo empleado en producir una unidad (horas / trabajador / unidad)

Eficiencia = En este modelo consideramos esta variable como factor de eficiencia de los operarios nuevos (curva de aprendizaje) – Solo la consideramos durante el primer periodo de producción del operario

Horas extras máx. = Cantidad máxima de horas extras que puede emplear un operario por periodo

Unidades subcontratadas máx. = Cantidad máxima de unidades que se pueden subcontratar por periodo

Inventario Inicial = Inventario Inicial dado en unidades

Costo normal = Costo de tiempo normal ($ / hora)

Costo extra = Costo de tiempo extra ($ / hora)

Costo de inventario = Costo de tener unidades en inventario ($ / unidad / periodo)

Costo de subcontratar = Costo de tercerizar la fabricación de unidades ($ / unidad)

Costo de contratar = Costo de contratar un operario ($ / operario)

Costo de despedir = Costo de despedir un operario ($ / operario)

Operarios = Número inicial de operarios

La siguiente formulación ha sido evaluada y validada en diversos programas solucionadores, como Solver, QM, WinQSB y Google Or-Tools.

Variables de decisión

x_i = Cantidad de unidades a producir en tiempo normal por operarios antiguos en el periodo i

xn_i = Cantidad de unidades a producir en tiempo normal por operarios nuevos en el periodo i

xz_i = Cantidad de unidades a producir en tiempo extra por operarios antiguos en el periodo i

xnz_i = Cantidad de unidades a producir en tiempo extra por operarios nuevos en el periodo i

c_i = Número de operarios a contratar en el periodo i

d_i = Número de operarios a despedir en el periodo i

oi_i = Número de operarios totales al inicio del periodo i

of_i = Número de operarios totales al final del periodo i

sub_i = Número de unidades a subcontratar en el periodo i

_invi = Número de unidades en inventario al final del periodo i

Variables de cálculos intermedios

P_i = Cantidad de unidades que puede producir en tiempo normal un operario antiguo en el periodo i

Pn_i = Cantidad de unidades que puede producir en tiempo normal un operario nuevo en el periodo i

H_i = Cantidad máxima de unidades que puede producir en tiempo extra un operario antiguo en el periodo i

Hc_i = Cantidad máxima de unidades que puede producir en tiempo extra un operario nuevo en el periodo i

Formulación de cálculos intermedios

P_i = (jornada laboral / tiempo unitario) * días del periodo i

Pn_i = P_i * Eficiencia

H_i = Horas extras máx. del periodo i / tiempo unitario

Hc_i = H_i * Eficiencia

Variables y entradas financieras

Costo unitario normal = Costo normal * Tiempo unitario

Costo unitario normal (operarios nuevos) = Costo normal * (Tiempo unitario / Eficiencia)

Costo unitario extra = Costo extra * Tiempo unitario

Costo unitario extra (operarios nuevos) = Costo extra * (Tiempo unitario / Eficiencia)

Restricciones de tiempo normal (Operarios antiguos)

( P_i * oi_i ) – x_i >= 0

Restricciones de tiempo normal (Operarios nuevos)

( Pn_i * c_i ) – xn_i >= 0

Restricciones de balance de operarios

Esta restricción define que los operarios al final de un periodo i = operarios inicial periodo i + 1

Para todos los i >= 1:

oi_i – of_i-1 = 0

Restricciones de balance para la contratación de operarios

Para todos los i >= 1:

of_i – oi_i – c_i + d_i = 0

Restricciones de cantidad inicial de operarios

Esta restricción nos indica que la cantidad inicial de operarios, es decir oi en periodo 0, es equivalente al dato de entrada operarios (El cual nos indica la cantidad inicial de operarios del problema). Esta restricción parece demasiado lógica, sin embargo es vital considerarla de acuerdo a los solucionadores que utilicemos.

oi₀ – operarios = 0

Restricciones de balance de operarios en el periodo 0 (periodo inicial)

of₀ – oi₀ – c₀ + d₀ = 0

Restricciones de límites de horas extras (operarios antiguos)

xz_i – ( H_i  * oi_i ) <= 0

Restricciones de límites de horas extras (operarios nuevos)

xnz_i – ( Hc_i  * c_i ) <= 0

Restricciones de límites de unidades a subcontratar

_subi – unidades subcontratadas máx. en el periodo i <= 0

Restricciones de balance de inventarios (periodo 1 en adelante)

Para todos los i >= 1:

Restricciones de balance de inventarios (periodo 0)

Restricciones de satisfacción de requerimientos (periodo 1 en adelante)

Para todos los i >= 1

x_i  + xn_i + xz_i  + xnz_i + sub_i  + inv_{i – 1} – requerimientos del periodo i >= 0

Restricciones de satisfacción de requerimientos (periodo 0)

x₀  + xn₀ + xz₀  + xnz₀ + sub₀  + inventario inicial – requerimientos del periodo 0 >= 0

Restricciones de no negatividad

Todas las variables pertenecen a los números reales enteros y sus valores deberán ser mayores o iguales a cero.

Función objetivo

Zmin = (costo unitario normal * x_i ) + (costo unitario normal de operarios nuevos * xn_i ) + (costo unitario extra * xz_i ) + (costo unitario extra operarios nuevos * xnz_i ) + (costo de subcontratar * sub_i ) + (costo de contratar * c_i ) + (costo de despedir * d_i ) + (costo de inventarios * inv_i )

La aplicación del anterior modelo arrojará la solución óptima por medio del algoritmo «branch and bound».

Caso de estudio: Aplicación de programación lineal en planeación agregada

Una compañía desea determinar su plan agregado de producción para los próximos 6 meses. Una vez utilizado el modelo de pronóstico más adecuado se establece el siguiente tabulado de requerimientos (no se cuenta con inventario inicial, y no se requiere de inventarios de seguridad).

Información relacionada con el negocio:

Jornada laboral: 8 horas / trabajador / día

Costo de contratar: $ 350 / trabajador

Costo de despedir: $ 420 / trabajador

Costo de tiempo normal (mano de obra): $ 6 / hora

Costo de tiempo extra (mano de obra): $8 / hora

Costo de mantenimiento de inventarios: $ 3 /unidad/ mes

Costo de subcontratar: $ 50 / unidad

Tiempo de procesamiento: 5 horas / trabajador / unidad

Jornada laboral: 8 horas / día

Número inicial de trabajadores: 20

Eficiencia de un trabajador nuevo el primer periodo: 90%

Cantidad máxima de horas extras por operario por mes: 8 horas/trabajador/mes

Capacidad máxima de suministro de unidades de subcontratación: 200 unidades/mes

Unidades: Toneladas.

---

Ya en la introducción del modelo hemos descrito la definición de las variables, la formulación de los cálculos intermedios, así mismo la formulación de las restricciones. Estas pueden utilizarse básicamente en cualquier solucionador.

En este caso vamos a utilizar un solucionador de programación basada en restricciones: Google OR-Tools. Para eso, vamos a programar nuestro modelo utilizando Python. No se preocupe si no cuenta con este programa, la idea es introducirnos de a poco en estas nuevas soluciones, por lo tanto utilizaremos un entorno virtual que podrás ejecutar sin la necesidad de realizar ninguna instalación.

Vamos a asumir que utilizarán el entorno virtual de Colaboratory, así que vayamos allá: Abrir cuaderno nuevo.

Paso 1: Instalar las librerías de Google Or Tools

Este paso debe realizarse solo si vamos a utilizar el cuaderno de Colaboratory:

!pip install ortools

Paso 2: Importar las librerías necesarias y declarar el solucionador

En este caso, solo importaremos la librería correspondiente al módulo de programación lineal de Google Or-Tools. Además, utilizaremos el solucionador SCIP (Solving Constraint Integer Programs), un solucionador de código abierto disponible que permite resolver problemas lineales mixtos (Google OR-Tools posee múltiples solucionadores):

from ortools.linear_solver import pywraplp

solver = pywraplp.Solver.CreateSolver('SCIP')

Paso 3: Datos de entrada

De acuerdo a los datos que nos plantea el problema, registramos las entradas del modelo:

#DATOS DE ENTRADA

periodos = [0, 1, 2, 3, 4, 5] #Periodos del plan, empezando desde el periodo 0
demanda = [2500, 1500, 3000, 1000, 2500, 2200] #Requerimintos de cada periodo
dias = [22, 19, 21, 21, 22, 20] #Días laborales de cada periodo
jornada_laboral = 8 #horas / trabajador / día
tiempo_unitario = 5 #horas / unidad
Eficiencia = 0.9 #Eficiencia de un trabajador nuevo periodo 1
horas_extras_max = [8, 8, 8, 8, 8, 8] #Cantidad máxima de horas extras por periodo
unidades_sub_max = [200, 200, 200, 200, 200, 200] #Cantidad máxima de unidades que se pueden subcontratar en el periodo i
inv_inicial = 0 #Unidades
costo_normal = 6 #Unidades monetarias / hora
costo_extra = 8 #Unidades monetarias / hora
costo_inventario = 3 #Unidades monetarias / periodo
costo_sub = 50 #Unidades monetarias / unidad
costo_contratar = 350 #Unidades monetarias / trabajador
costo_despedir = 420 #Unidades monetarias / trabajador
operarios = 20 #Número inicial de trabajadores

Paso 4: Definir y formular los cálculos intermedios

De acuerdo a la formulación que ya mostramos de nuestro modelo, se definirán aquellos cálculos intermedios necesarios. Recordemos la formulación que teníamos definida:

P_i = (jornada laboral / tiempo unitario) * días del periodo i

Pn_i = P_i * Eficiencia

H_i = Horas extras máx. del periodo i / tiempo unitario

Hc_i = H_i * Eficiencia

Si realizamos los cálculos de forma manual, podemos completar una tabla como la siguiente:

Veamos por ejemplo, el periodo 0 (periodo inicial).

P₀ (mes 1) = (8 / 5) * 22

P₀ (mes 1) = 35,20

Ahora veamos cómo podemos programar este cálculo en nuestro modelo (mediante un ciclo):

P= [] #Cantidad de unidades que puede producir un operario en el periodo i
for i in range(len(periodos)):
    P.append((jornada_laboral / tiempo_unitario) * dias[i])

De esta forma efectuamos el cálculo para cada período. Veamos lo que pasaría imprimimos la variable P:

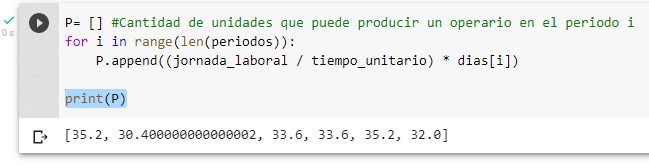Podemos corroborar cómo obtenemos los mismos resultados que se encuentran consignados en el tabulado. Ahora completaremos los cálculos intermedios restantes:

Pn= []#Cantidad de unidades que puede producir un operario nuevo en el periodo i
for i in range(len(periodos)):
    Pn.append(P[i] * Eficiencia)
    
H= []#Cantidad máxima de unidades que puede producir un operario en el periodo i con horas extras
for i in range(len(periodos)):
    H.append(horas_extras_max[i] / tiempo_unitario)
    
Hc= []#Cantidad máxima de unidades que puede producir un operario en el periodo i con horas extras
for i in range(len(periodos)):
    Hc.append(H[i] * Eficiencia)

Paso 5: Definir las variables de decisión

En este paso definiremos cada variable de decisión del modelo, definiremos también su naturaleza y su rango de valores: entera, mayor o iguala cero (desde 0 hasta infinito).

#Variables de decisión

x= {} #Unidades a producir en el periodo i
for i in range(len(periodos)):
    x[i] = solver.IntVar(0, solver.infinity(), '')
    
xn= {} #Unidades a producir por operarios nuevos en el periodo i
for i in range(len(periodos)):
    xn[i] = solver.IntVar(0, solver.infinity(), '')
    
xz= {} #Unidades a producir en tiempo extra en el periodo i
for i in range(len(periodos)):
    xz[i] = solver.IntVar(0, solver.infinity(), '')
    
xnz= {} #Unidades a producir en tiempo extra por operarios nuevos en el periodo i
for i in range(len(periodos)):
    xnz[i] = solver.IntVar(0, solver.infinity(), '')
    
c= {} #Operarios a contratar en el período i
for i in range(len(periodos)):
    c[i] = solver.IntVar(0, solver.infinity(), '')

d= {} #Operarios a despedir en el período i
for i in range(len(periodos)):
    d[i] = solver.IntVar(0, solver.infinity(), '')
    
sub= {} #Unidades a subcontratar en el periodo i
for i in range(len(periodos)):
    sub[i] = solver.IntVar(0, solver.infinity(), '') 
    
inv= {} #Unidades en inventario al final del periodo i
for i in range(len(periodos)):
    inv[i] = solver.IntVar(0, solver.infinity(), '') 
    
oi= {} #Número de operarios totales al inicio del periodo i
for i in range(len(periodos)):
    oi[i] = solver.IntVar(0, solver.infinity(), '') 
    
of= {} #Número de operarios totales al final del periodo i
for i in range(len(periodos)):
    of[i] = solver.IntVar(0, solver.infinity(), '') 

En el código anterior, y ya que cada variable debe definirse para cada periodo del plan agregado, utilizamos ciclos para su definición. Este ciclo tiene un rango determinado por el número de periodos, de esta manera, ya que tenemos 6 periodos, por ejemplo, en la definición de la variable Xi, tendremos las siguientes variables definidas: x₀, x₁, x₂, x₃, x₄, x₅ . Así mismo sucede con las variables restantes.

Desde luego, existe la posibilidad de definir cada una de las variables de forma individual, sin embargo el proceso sería algo tedioso, y sería algo así:

x[0] = solver.IntVar(0, solver.infinity(), »)

x[1] = solver.IntVar(0, solver.infinity(), »)

x[2] = solver.IntVar(0, solver.infinity(), »)

x[3] = solver.IntVar(0, solver.infinity(), »)

x[4] = solver.IntVar(0, solver.infinity(), »)

x[5] = solver.IntVar(0, solver.infinity(), »)

Por esta razón utilizamos ciclos para tal efecto.

Paso 6: Formulación de variables de costo

#Formulación de variables financieras (Costos)
costo_unitario_normal = costo_normal * tiempo_unitario
costo_unitario_normal_nuevo = costo_normal * (tiempo_unitario / Eficiencia) 
costo_unitario_extra = costo_extra * tiempo_unitario
costo_unitario_extra_nuevo = costo_extra * (tiempo_unitario / Eficiencia) 

Paso 7: Restricciones del modelo

Utilizando la misma metodología de ciclos para recorrer los periodos del plan, formulamos nuestras restricciones. Estas restricciones son exactamente las mismas que formulamos de manera algebraica en el planteamiento general de nuestro modelo.

#RESTRICCIONES DEL MODELO

# Restricciones de tiempo normal (Producción normal)
for i in range(len(periodos)):
    solver.Add(((P[i] * oi[i]) - x[i]) >= 0)

# Restricciones de tiempo normal (Producción normaml - operarios nuevos)
for i in range(len(periodos)):
    solver.Add(((Pn[i] * c[i]) - xn[i]) >= 0)
    
# Restricciones de balance (operarios al final de un periodo i = operarios inicial periodo i + 1)
for i in range(1, len(periodos)):
    solver.Add(oi[i] - of[i-1] == 0)
    
# Restricciones de balance para la contratación de operarios (periodo i en adelante)
for i in range(1, len(periodos)):
    solver.Add(of[i] - oi[i] - c[i] + d[i] == 0)
    
# Restricción de cantidad inicial de operarios
solver.Add(oi[0] - operarios == 0)
    
# Restricciones de balance de operarios periodo 0
solver.Add(of[0] - oi[0] - c[0] + d[0] == 0)
    
# Restricciones límite de horas extras operarios antiguos
for i in range(len(periodos)):
    solver.Add(xz[i] -(H[i] * oi[i]) <= 0)
    
# Restricciones límite de horas extras operarios nuevos
for i in range(len(periodos)):
    solver.Add(xnz[i] -(Hc[i] * c[i]) <= 0)
    
# Restricciones límite de unidades a subcontratar
for i in range(len(periodos)):
    solver.Add(sub[i] - unidades_sub_max[i] <= 0) 

# Restricciones límite de balance de inventarios periodo 1 en adelante 
for i in range(1, len(periodos)): 
    solver.Add(inv[i-1] + x[i] + xn[i] + xz[i] + xnz[i] + sub[i] - demanda[i] - inv[i] == 0) 

# Restricciones límite de balance de inventarios periodo 0 
solver.Add(inv_inicial + x[0] + xn[0] + xz[0] + xnz[0] + sub[0] - demanda[0] - inv[0] == 0) 

# Restricciones de satisfacción de demanda periodo 1 en adelante 
for i in range(1, len(periodos)): 
    solver.Add(x[i] + xn[i] + xz[i] + xnz[i] + sub[i] + inv[i-1] - demanda[i] >= 0)
    
# Restricciones límite de balance de inventarios periodo 0
solver.Add(x[0] + xn[0] + xz[0] + xnz[0] + sub[0] + inv_inicial - demanda[i] >= 0)

Paso 8: Definir la función objetivo

#FUNCIÓN OBJETIVO MINIMIZAR
objective_terms = []
for i in range(len(periodos)):
    objective_terms.append((costo_unitario_normal * x[i]) + (costo_unitario_normal_nuevo * xn[i]) + (costo_unitario_extra * xz[i]) + (costo_unitario_extra_nuevo * xnz[i]) + (costo_sub * sub[i]) + (costo_contratar * c[i]) + (costo_despedir * d[i]) + (costo_inventario * inv[i]))
solver.Minimize(solver.Sum(objective_terms))  

Paso 9: Invocar al solucionador

A continuación daremos la orden al programa de resolver el modelo.

#Invocar al solucionador
status = solver.Solve()

Paso 10: Configurar las salidas del modelo

Este paso lo verán quizá confuso; y la verdad no lo es tanto. Toda vez que el modelo está resuelto, podemos configurar la salida que queramos en cualquier momento; eso sí, hemos desarrollado unas líneas de código que pueden resultar extensas, con el fin de organizar los datos de salida. Por ejemplo, hemos definido encabezados para los datos, y otras cuestiones de forma.

Si usted desea, por ejemplo, tan solo conocer el valor total del plan agregado, puede introducir las siguientes líneas:

print('\nValor total del plan (FO) =', solver.Objective().Value())

Al ejecutar esta línea tendremos el siguiente resultado:

Las siguientes líneas nos proporcionarán la información relevante de forma organizada:

if status == pywraplp.Solver.OPTIMAL:
    print('\nSOLUCIÓN: ')        
    print('\nPLAN DE PRODUCCIÓN \n')
    print('|{:^20}|{:^20}|{:^20}|{:^20}|{:^20}|{:^20}|'.format(
      'Período',
      'Producción (TN)',
      'TN (Op. Nuevos)',
      'Producción (HE)',
      'HE (Op. Nuevos)',
      'Uni. Subcon'))
    
    for i in range(len(periodos)):
        print('|{:^20}|{:^20}|{:^20}|{:^20}|{:^20}|{:^20}|'.format(
          i,
          x[i].solution_value(),
          xn[i].solution_value(),
          xz[i].solution_value(),
          xnz[i].solution_value(),
          sub[i].solution_value()))
    print('\nProduccción (TN): Cantidad de unidades a producir en tiempo normal')
    print('TN (Op. Nuevos): Cantidad de unidades a producir en tiempo normal con operarios nuevos')
    print('Producción (HE): Cantidad de unidades a producir en tiempo extra')
    print('HE (Op. Nuevos): Cantidad de unidades a producir en tiempo extra con operarios nuevos')
    print('Uni. Subcon: Cantidad de unidades a subcontratar')
    print('\nCOSTOS \n')
    print('|{:^20}|{:^20}|'.format(
          'Período',
          'Costo'))  
    costo = []
    for i in range(len(periodos)):
        costo.append((costo_unitario_normal * x[i].solution_value()) + (costo_unitario_normal_nuevo * xn[i].solution_value()) + (costo_unitario_extra * xz[i].solution_value()) + (costo_unitario_extra_nuevo * xnz[i].solution_value()) + (costo_sub * sub[i].solution_value()) + (costo_contratar * c[i].solution_value()) + (costo_despedir * d[i].solution_value()) + (costo_inventario * inv[i].solution_value()))
        print('|{:^20}|{:^20.2f}|'.format(
          i,
          costo[i]))
    print('\nValor total del plan (FO) =', solver.Objective().Value())
    print('Costo unitario del tiempo normal = {0} unidades monetarias / h'.format(costo_unitario_normal))
    print('Costo unitario del tiempo normal (Operarios nuevos)= {0:.2f} unidades monetarias / h'.format(costo_unitario_normal_nuevo))
    print('Costo unitario del tiempo extra= {0} unidades monetarias / h'.format(costo_unitario_extra))
    print('Costo unitario del tiempo extra (Operarios nuevos)= {0:.2f} unidades monetarias / h'.format(costo_unitario_extra_nuevo))
    print('\nINVENTARIOS \n')
    print('|{:^20}|{:^20}|'.format(
          'Período', 
          'Inv. final'))  
    for i in range(len(periodos)):    
        print('|{:^20}|{:^20}|'.format(
          i,
          inv[i].solution_value()))
    print('\nFUERZA LABORAL (OPERARIOS)\n')
    print('|{:^20}|{:^20}|{:^20}|{:^20}|{:^20}|'.format(
          'Período', 
          'Cantidad inicial',
          'Contrataciones',
          'Despidos',
          'Cantidad final'))  
    for i in range(len(periodos)):    
        print('|{:^20}|{:^20}|{:^20}|{:^20}|{:^20}|'.format(
          i,
          oi[i].solution_value(),
          c[i].solution_value(),
          d[i].solution_value(),
          of[i].solution_value()))
   
    vector_i=[]
    vector_x=[]
    vector_xn=[]
    vector_xz=[]
    vector_xnz=[]
    vector_sub=[]    
    
    for i in range (len(periodos)):
        vector_i.append(i)
        vector_x.append(x[i].solution_value())
        vector_xn.append(xn[i].solution_value())
        vector_xz.append(xz[i].solution_value())
        vector_xnz.append(xnz[i].solution_value())
        vector_sub.append(sub[i].solution_value())    
    
    datos = {}
    
    datos['Periodo'] = vector_i
    datos['Producción (TN)'] = vector_x
    datos['TN (Op. Nuevos)'] = vector_xn
    datos['Producción (HE)'] = vector_xz
    datos['HE (Op. Nuevos)'] = vector_xnz
    datos['Uni. Subcon'] = vector_sub
      
else:
  if status == solver.FEASIBLE:
    print('Se encontró una solución potencialmente subóptima.')
  else:
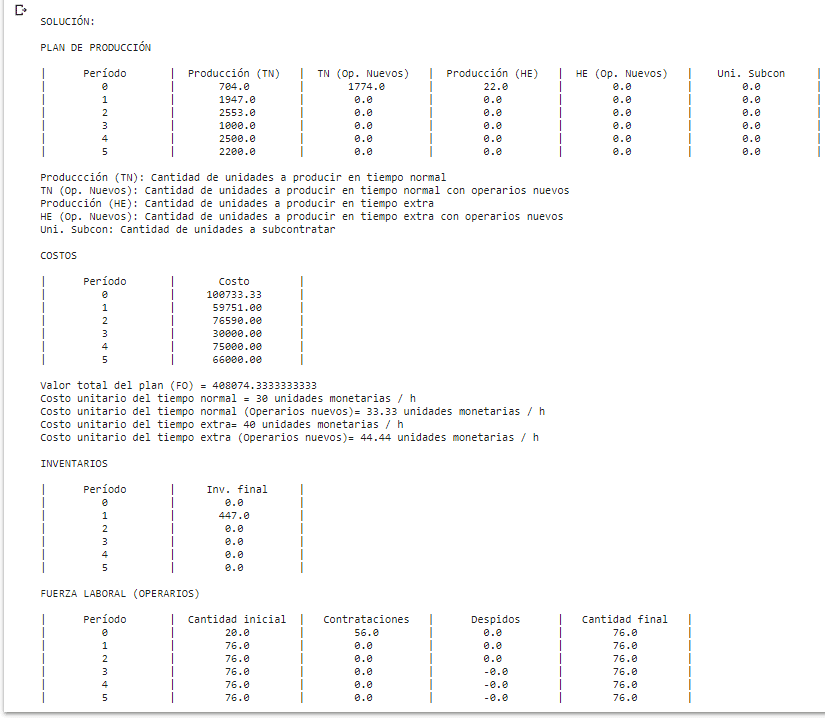
    print('El problema no tiene solución óptima.')

Al ejecutar el modelo tendremos:

Puedes acceder y ejecutar el modelo desde Planeación Agregada mediante Programación Lineal.

El tiempo empleado por el solucionador es inferior a 1 segundo de procesamiento. Dada la potencia del solucionador Google Or Tools y la capacidad de procesamiento del entorno virtual.

El valor objetivo hallado es: 408074,33

Parte de la utilidad de este desarrollo es la posibilidad de integrarse con diversas fuentes de información. Puede, por ejemplo, tomar datos desde diversos archivos en entornos locales o externos. De igual forma puede exportar la información obtenida.

Utilizando este modelo y su formulación en Solver de Microsoft Excel

El mismo modelo que hemos desarrollado en Python ha sido formulado en Microsoft Excel para su resolución mediante Solver. De acuerdo a los parámetros genéricos de Solver, sin modificar límites de búsqueda, hemos obtenido una solución equivalente a: 410498, empleando aproximadamente 50 segundos para llegar a ella.

Podemos observar entonces que la solución obtenida mediante Google Or-Tools satisface mucho más el criterio de optimización, así mismo alcanza la solución en un tiempo mucho menor.

¿A qué puede deberse esa diferencia entre las soluciones obtenidas mediante ambos solucionadores? Principalmente a la tolerancia predeterminada de los solucionadores de Solver para las restricciones de variables enteras. Es posible incluso, en el cuadro de opciones de Solver configurar esta tolerancia como 0 para obtener mejores resultados. Lo hemos hecho y hemos alcanzado 419601. Sin embargo, el tiempo de búsqueda puede tardar minutos.