¿Cómo calcular una matriz de distancias para modelar un VRP?
Tal como lo hemos abordado ampliamente, una de las aplicaciones más importantes del modelamiento de Cadenas de Suministro, es el diseño de red de abastecimiento, y dentro de esta categoría, el diseño de rutas de transporte (enrutamiento de vehículos).
Los problemas de enrutamiento de vehículos (routing), se encuentran clasificados como problemas de optimización combinatoria, y esto producto de que la cantidad de rutas posibles en un modelo básico, se encuentra determinado por la ecuación (n – 1)!, donde n, es igual al número de ubicaciones que componen el problema de enrutamiento.
Ahora bien, no solo la resolución de los problemas de enrutamiento es considerada como compleja, también lo es la fase preliminar en la que debemos levantar la información de entrada del modelo (inputs), específicamente, la matriz de distancias.
La forma más básica de un modelo VRP, requiere para su resolución la siguiente información mínima de entrada:
- Número de vehículos
- Un depósito
- Matriz de distancias
La matriz de distancias es un tabulado que registra la longitud entre cada uno de los nodos del modelo, incluido el nodo depósito. Su tamaño será n x n (siendo n el número de nodos del modelo). Asumiendo, por ejemplo, que tenemos un problema que se compone de 1 depósito y 19 ubicaciones, el modelo requerirá de una matriz de distancias con 400 datos.
Recuerdo que cuando abordamos por primera vez este tema en la Universidad, en mi etapa de estudiante, se nos mencionó enfáticamente la complejidad que subyace en este tipo de modelos: El procesamiento, el levantamiento de datos, la consideración de ubicaciones reales, etc.
Pues bien, han pasado algunos años desde entonces, y todo cambió. El modelamiento de este tipo de problemas, la integración con sistemas de información geográfica, la posibilidad de automatizar procesos de captura de información. ¡Todo!
En artículos anteriores hemos abordado modelos robustos para la resolución de problemas VRP y algunas de sus extensiones (CVRP, por ejemplo). El objetivo de este artículo será la de utilizar funciones espaciales de Python, para obtener una matriz de distancias de acuerdo a ubicaciones reales, con el propósito de resolver un modelo VRP básico.
Caso de aplicación
La Secretaría de Educación de Santiago de Cali, tiene dentro de sus funciones, distribuir el material pedagógico a las diferentes instituciones de formación de la ciudad. La distribución del material se realiza todos los lunes, y para ello, la Secretaría cuenta con dos vehículos con capacidad suficiente para transportar todo el material. El depósito del material (lugar desde donde salen y deben regresar los vehículos), se encuentra en la Alcaldía de Cali; y las instituciones que deben visitarse son 60. Tal como podemos apreciar en la siguiente tabla:
| Nodo | Lugar | Latitud | Longitud |
| 0 | Secretaría de Educación – Alcaldía | 3,454431875 | -76,53421433 |
| 1 | Comfandi San Nicolás | 3,453591118 | -76,52254886 |
| 2 | Mayor de Santiago de Cali | 3,451577758 | -76,51023216 |
| 3 | Municipal Comfandi | 3,448107915 | -76,51074714 |
| 4 | Internado San Carlos | 3,446994135 | -76,51525325 |
| 5 | León de Greiff | 3,447979402 | -76,49993247 |
| 6 | Nuestra Señora de la Anunciación | 3,445152112 | -76,49641342 |
| 7 | Fernando de Aragón | 3,437355603 | -76,51383704 |
| 8 | Casa Evangélica | 3,437955337 | -76,52299947 |
| 9 | San Alberto Magno | 3,433028941 | -76,52707643 |
| 10 | Santa María Goretty | 3,433414486 | -76,50720662 |
| 11 | San Alberto Magno | 3,433157456 | -76,5267331 |
| 12 | San Ignacio de Loyola | 3,431786629 | -76,51733464 |
| 13 | Nuestro Futuro | 3,430629992 | -76,50360174 |
| 14 | Sabio Caldas | 3,429087807 | -76,51660508 |
| 15 | CREAD | 3,425060978 | -76,51488847 |
| 16 | Licomtec | 3,416664559 | -76,51673383 |
| 17 | Nuestra Señora De La Providencia | 3,419534772 | -76,49591989 |
| 18 | Real Suizo | 3,415208029 | -76,49323768 |
| 19 | Nuevo Edén | 3,415722099 | -76,53383559 |
| 20 | Católico | 3,413066071 | -76,53984374 |
| 21 | Santa María Stella | 3,427031556 | -76,55134505 |
| 22 | Santa Isabel | 3,40805355 | -76,50817223 |
| 23 | Compartir | 3,431957663 | -76,47495575 |
| 24 | Lancaster | 3,400770816 | -76,55177421 |
| 25 | Parroquial Divino Salvador | 3,397086588 | -76,54259033 |
| 26 | Reyes Católicos | 3,393316667 | -76,53735466 |
| 27 | Liceo Anglo del Valle | 3,387318719 | -76,51975937 |
| 28 | Laurence | 3,383420238 | -76,52078934 |
| 29 | Los Almendros | 3,381278208 | -76,52023144 |
| 30 | Bautista | 3,37720834 | -76,52327843 |
| 31 | Lacordaire | 3,378150837 | -76,54460736 |
| 32 | General José María Córdoba | 3,393573314 | -76,54932805 |
| 33 | El Hogar | 3,390745864 | -76,5503151 |
| 34 | Americano | 3,379093255 | -76,54688187 |
| 35 | Santa Filomena | 3,401969935 | -76,51345082 |
| 36 | Tomás Vasconi | 3,403040928 | -76,5173132 |
| 37 | República del Salvador | 3,404454636 | -76,52143308 |
| 38 | Los Andes | 3,429601077 | -76,53761216 |
| 39 | Villacolombia | 3,445493943 | -76,50169202 |
| 40 | Las Américas | 3,449220822 | -76,50594064 |
| 41 | Santa Fe | 3,442238267 | -76,50988885 |
| 42 | Evaristo García | 3,440781776 | -76,51752778 |
| 43 | Alfredo Vásquez Cobo | 3,435598366 | -76,5164549 |
| 44 | Ciudad de Cali | 3,431143181 | -76,51272126 |
| 45 | INEM | 3,482761991 | -76,49976083 |
| 46 | Olaya Herrera | 3,478178519 | -76,51280709 |
| 47 | Guillermo Valencia | 3,47449459 | -76,5136654 |
| 48 | José Ignacio Rengifo | 3,471624543 | -76,5136654 |
| 49 | Santo Tomás | 3,45830227 | -76,5164549 |
| 50 | La Merced | 3,46271449 | -76,5024645 |
| 51 | Pedro Antonio Molina | 3,482804827 | -76,48761579 |
| 52 | Santa Librada | 3,46228612 | -76,52302095 |
| 53 | República de Israel | 3,463656904 | -76,51053258 |
| 54 | San Vicente Paul | 3,466227117 | -76,50950261 |
| 55 | Manuel María Mallarino | 3,456760129 | -76,48851701 |
| 56 | Sebastián de Belalcazar | 3,460229941 | -76,48521253 |
| 57 | Liceo Departamental | 3,423860462 | -76,5385563 |
| 58 | Libardo Madrid | 3,422061154 | -76,54383489 |
| 59 | Metropolitano Santa Anita | 3,401691038 | -76,54218265 |
| 60 | San José | 3,396935816 | -76,55031511 |
Se desea desarrollar un plan de rutas para cada uno de los vehículos que logre minimizar la distancia total recorrida, al tiempo que asegure la visita de todos los colegios.
¿Qué necesitaremos?
En el desarrollo de este ejercicio emplearemos:
- Colaboratory: Este es un entorno de programación y ejecución virtual de Python desarrollado por Google. Nos permitirá no tener la necesidad de realizar ninguna instalación en nuestros equipos. Todo lo que desarrollemos lo ejecutaremos en un cuaderno virtual.
- Python: Este será el lenguaje de programación que vamos a utilizar, y advertimos: No es necesario tener conocimientos previos, y el objetivo del artículo no es convertirnos en programadores expertos. Utilizaremos fragmentos de códigos, librerías disponibles, y explicaremos lo necesario para configurar nuestro desarrollo de acuerdo a los objetivos específicos de nuestros modelos.
- SkLearn: Las librerías son a Python, lo que las apps son a un teléfono celular. Esta es quizá una de las características más a tractivas de este lenguaje: Casi que existe una librería para cada necesidad. En este caso, SKLearn, es una librería que integra un conjunto de métodos de aprendizaje automático y minería de datos. En este caso utilizaremos sus funciones para cálculo de distancias entre pares.
- Pandas: Es un paquete de Python que proporciona estructuras de datos rápidas, y flexibles, diseñadas para que el trabajo con datos estructurados (tabulares, multidimensionales, potencialmente heterogéneos) y de series de tiempo sea fácil e intuitivo.
- Numpy: Es una librería que nos permitirá efectuar operaciones matriciales en Python.
- Math: Es una librería que contiene un conjunto de funciones matemáticas básicas.
Paso 1: Crear el entorno de trabajo en Colaboratory
Lo primero que vamos a hacer consiste en crear un entorno de trabajo en Google Colaboratory, así que vayamos allá: Abrir cuaderno nuevo.
Verán que tienen un lienzo para programar el modelo, así que en este cuaderno podemos ir generando las líneas de código que explicaremos en los pasos siguientes.
Paso 2: Importar las librerías necesarias
Respecto a las librerías, en la introducción del artículo hicimos una descripción de la funcionalidad de cada una, veamos como importarlas en nuestro entorno:
from sklearn.neighbors import DistanceMetric
from math import radians
import pandas as pd
import numpy as npDe esta manera, tenemos todo lo necesario para empezar a desarrollar nuestro código.
Paso 3: Importar los datos desde Excel
De acuerdo a las necesidades del modelo, podemos desarrollar un código que permita la entrada manual de la información, la captura de los datos desde entornos digitales (Internet, por ejemplo), o podemos, desde luego, alimentar nuestro modelo con información contenida en documentos externos, como es el caso de un archivo de Microsoft Excel.
Esta puede considerarse como una de las ventajas de utilizar Python, su capacidad de integrarse con cualquier fuente de datos. En nuestro caso, toda la información se encuentra contenida en un documento de Excel, el cual presenta el siguiente formato:
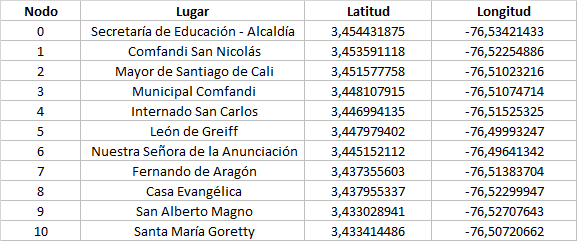
Utilizaremos ubicaciones reales, y para eso emplearemos las coordenadas de latitud y longitud.
En Colaboratory, el siguiente fragmento permitirá cargar un archivo al entorno de ejecución:
from google.colab import files
uploaded = files.upload()
for fn in uploaded.keys():
print('User uploaded file "{name}" with length {length} bytes'.format(
name=fn, length=len(uploaded[fn])))Al ejecutar este fragmento de código, se abrirá una ventana emergente del explorador que permitirá cargar nuestra base de datos, en nuestro caso el archivo tienen el nombre de colegios.xlsx.
La siguiente línea de código permitirá almacenar los datos contenidos en el documento en un Dataframe de nuestro entorno, dentro de la variable data.
#Leer el documento de Excel y almacenar los datos en la variable data
data = pd.read_excel('colegios.xlsx')Podemos en cualquier momento confirmar si la carga de los datos se ha realizado correctamente, para eso imprimiremos las primeras cinco filas del DataFrame:
data.head()Al ejecutar esta instrucción tenemos la siguiente salida (Una vista de las 5 primeras filas del marco de datos):
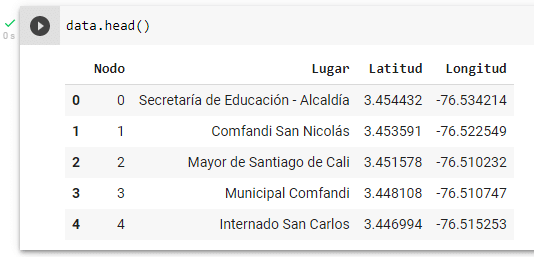
Podemos observar que los datos han sido perfectamente cargados, y que ahora se encuentran almacenados en la variable (DataFrame): data.
Paso 4: Convertir las coordenadas de latitud y longitud en radianes
La mayor parte de las funciones de cálculo de distancias de Sklearn (Scipy) toman las entradas como radianes. Por esta razón, debemos convertir las coordenadas en radianes.
data['Latitud'] = np.radians(data['Latitud'])
data['Longitud'] = np.radians(data['Longitud'])
#Creamos una matriz bidimensional con la latitud y la longitud en radianes
data[['Latitud','Longitud']].to_numpy()Al ejecutar estas líneas, las coordenadas quedarán convertidas en radianes.
Paso 5: Declarar el tipo de métrica de distancias que se utilizará
En este punto quiero detenerme para mencionar que existen decenas de funciones métricas de distancia rápida. Algunas de las más utilizadas son destinadas a espacios vectoriales de valor real, como: distancias euclidianas, distancias de Manhattan, etc. Prácticas cuando se emplean con coordenadas cartesianas.
En nuestro caso, ya que utilizamos ubicaciones reales y contamos con coordenadas de latitud y de longitud, podemos emplear una función de distancia de vectores bidimensionales que considere la curvatura de la tierra; tal es el caso de las Distancias Haversine (Semiverseno).
Como la Tierra es casi esférica, la fórmula Haversine proporciona una buena aproximación de la distancia entre dos puntos de la superficie terrestre, con un error de menos del 1% en promedio.
Si quieren conocer la fórmula empleada para el cálculo de cada distancia haversine:
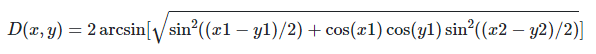
Para efectos de nuestro desarrollo, utilizaremos la librería SKLearn para calcular nuestras distancias. Veamos:
dist = DistanceMetric.get_metric('haversine')
dist.pairwise(data[['Latitud','Longitud']].to_numpy())*6373El fragmento anterior crea un objeto con métricas haversine, y luego utiliza la función pairwise(), para calcular la distancia entre cada uno de los elementos de la matriz (nodos). Cada distancia calculada multiplica el escalar 6373 (radio esférico de la tierra), para calcular las distancias en kilómetros (Para millas multiplicar por 3798).
Paso 6: Crear un marco de datos (tabulado) de matriz de distancias
Una vez que ejecutemos el paso anterior, tendremos nuestras distancias entre nodos calculadas; lo que haremos en este paso será organizar dichos valores en forma de marco de datos o tabulado, obteniendo nuestra matriz de distancias.
distance_matrix = pd.DataFrame(dist.pairwise(data[['Latitud','Longitud']].to_numpy())*6373)
distance_matrix.head()Al ejecutar esta instrucción tenemos la siguiente salida (Una vista de las 5 primeras filas del marco de datos):
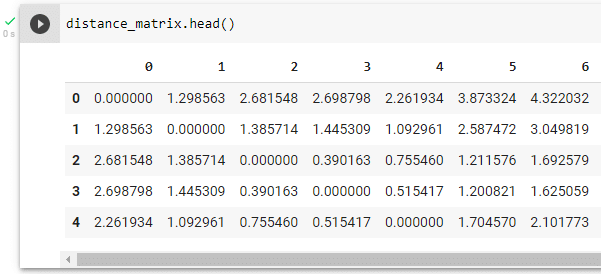
Podemos imprimir la matriz completa:
print(distance_matrix)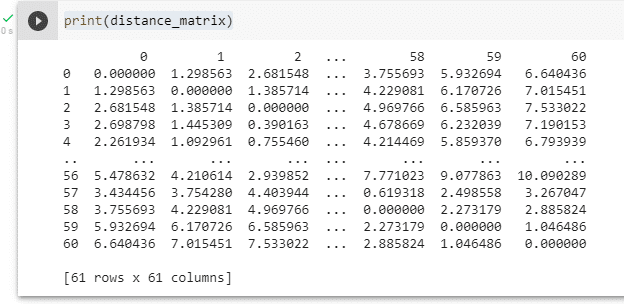
Hasta este punto hemos logrado nuestro objetivo principal, que era obtener una matriz de distancias de forma automática tomando como base las coordenadas de longitud y latitud de un conjunto de nodos. Específicamente hemos obtenido 3721 valores de distancia en cuestión de segundos (empleando la métrica haversine).
Lógicamente, estos valores de referencia en la práctica presentan algunas desventajas, como, por ejemplo, la dificultad subyacente de atravesar las ciudades por lugares diferentes que las vías dispuestas para ello. Sin embargo, estos valores pueden ser muy útiles como datos de entrada de un modelo VRP para obtener la secuencia del plan de rutas.
Lo siguiente que haremos, para finalizar nuestro caso de aplicación, será utilizar la matriz de distancias obtenida, en un modelo VRP básico (Si desea profundizar en el modelo, visite el artículo).
Paso 7: Instalar Google Or Tools
Es necesario instalar la librería de Google Or Tools en nuestro entorno de Colaboratory para poder utilizar nuestro modelo VRP.
!pip install ortoolsAl ejecutar esta instrucción instalaremos nuestro solucionador del modelo de enrutamiento.
Paso 8: Incorporar el modelo VRP (Previamente formulado)
Como ya lo mencionamos, contamos con un modelo debidamente formulado para resolver problemas VRP básicos. Lo único que modificaremos serán los datos de entrada: Matriz de distancias (distance_matrix), Número de vehículos (2), Depósito (Nodo 0).
"""Problema de enrutamiento de vehículos simple (VRP)
Autor: MSc. Ing. Bryan Salazar López 2021
"""
from ortools.constraint_solver import routing_enums_pb2
from ortools.constraint_solver import pywrapcp
def create_data_model():
"""Datos de entrada del modelo"""
#Llamaremos la matriz de distancia previamente obtenida
#Emplearemos dos vehículos como lo indica el problema
#Definiremos el nodo 0 como el depósito (Secretaría)
data = {}
data['matriz_distancias'] = distance_matrix
data['num_vehiculos'] = 2
data['deposito'] = 0
return data
def print_solution(data, manager, routing, solution):
"""Imprime la solución sobre la consola"""
max_route_distance = 0
for vehicle_id in range(data['num_vehiculos']):
index = routing.Start(vehicle_id)
plan_output = 'Ruta para el vehículo {}:\n'.format(vehicle_id)
route_distance = 0
while not routing.IsEnd(index):
plan_output += ' {} -> '.format(manager.IndexToNode(index))
previous_index = index
index = solution.Value(routing.NextVar(index))
route_distance += routing.GetArcCostForVehicle(
previous_index, index, vehicle_id)
plan_output += '{}\n'.format(manager.IndexToNode(index))
plan_output += 'Distancia de la ruta: {}km\n'.format(route_distance)
print(plan_output)
max_route_distance += route_distance
max_route_distance = max(route_distance, max_route_distance)
print('Distancia total de todas las rutas: {}km'.format(max_route_distance))
def main():
"""Punto de entrada del programa"""
# Invocar la data de entrada.
data = create_data_model()
# Crea el administrador del índice de rutas.
manager = pywrapcp.RoutingIndexManager(len(data['matriz_distancias']),
data['num_vehiculos'], data['deposito'])
# Crea el modelo de enrutamiento.
routing = pywrapcp.RoutingModel(manager)
# Crea y registra una devolución de llamada de distancia.
def distance_callback(from_index, to_index):
"""Retorna la distancia entre dos nodos."""
# Convierte desde la variable de ruta Index hasta la matriz de distancia NodeIndex.
from_node = manager.IndexToNode(from_index)
to_node = manager.IndexToNode(to_index)
return data['matriz_distancias'][from_node][to_node]
transit_callback_index = routing.RegisterTransitCallback(distance_callback)
# Define el costo de cada arco.
routing.SetArcCostEvaluatorOfAllVehicles(transit_callback_index)
# Adhiere la dimensión de distancia.
dimension_name = 'Distancia'
routing.AddDimension(
transit_callback_index,
0, # Sin holgura
3000, # Distancia máxima de viaje del vehículo
True, # Iniciar el acumulador en cero
dimension_name)
distance_dimension = routing.GetDimensionOrDie(dimension_name)
distance_dimension.SetGlobalSpanCostCoefficient(100)
# Configurar los parámetros de búsqueda.
search_parameters = pywrapcp.DefaultRoutingSearchParameters()
search_parameters.first_solution_strategy = (
routing_enums_pb2.FirstSolutionStrategy.PATH_CHEAPEST_ARC)
# Solucionador del problema.
solution = routing.SolveWithParameters(search_parameters)
# Imprimir la solución en la consola.
if solution:
print_solution(data, manager, routing, solution)
else:
print('No se encuentra solución !')
if __name__ == '__main__':
main()Al ejecutar el modelo tendremos:

Un plan de rutas para los dos vehículos que parten desde los depósitos (ahí mismo finalizan sus recorridos), y visitan la totalidad de los nodos. La distancia total optimizada es equivalente a 33 km.
Por último, también es posible exportar la matriz de distancias que hemos obtenido, para eso utilizaremos el siguiente fragmento:
distance_matrix.to_csv('distance_matrix.csv')
files.download('distance_matrix.csv')Los contribuciones de la comunidad han revelado que el modelo VRP de Or Tools maneja valores enteros para las distancias en la matriz. Esto significa que, por ejemplo, una distancia de 0.58 km se trataría como un entero, lo que puede causar pérdida de precisión en los resultados. Por esta razón, recomendamos trabajar con la unidad más pequeña de longitud posible, como metros, y convertir las distancias antes de ejecutar el modelo de ruteo. Por ejemplo, 0.58 km se convertiría en 580 metros, evitando pérdida de precisión. Además, es importante tener en cuenta que esto afectaría la distancia máxima del viaje del vehículo, la cual debemos modificar, en consecuencia.
El código completo de este desarrollo lo puedes encontrar en nuestro cuaderno: Matriz de distancias para modelar un VRP.




Hola, en primer lugar, felicitarte por el artículo que me ha parecido muy interesante y en segundo lugar ¡volverte a felicitarte por la claridad del mismo y utilidad! aunque realmente si lo utilizo es con fines didácticos en clase como aplicación práctica de programación.
Hola Simón. Ha sido todo un gusto leer tu comentario.
Gracias por el mensaje.
Excelente contribución y mejor aún con el código disponible y ejemplos reales. Si tuvieras algún ejemplo para equipos de servicio de trademarketing en punto de venta sería genial. Hay variables que considerar como el tiempo de servicio en el pdv, traslados, rutas que varían de una semana a otra, etc.
Estimado, existe un problema en el uso de esta solucion y es que las clases que utiliza or-tool como el agente de llamada de transito o distancia etc, en sus resultados devuelven enteros, asi que al utilizar numeros flotantes como es el caso de la matriz de distancia los valores menores a 1 , como 0.58 o 0.40 o 0.98 que al sumar representan una cantidad importanten no son calculados ya que no admite valores flotantes esto incluye cualquier valor flotante pues un 2.48 es redondeado a 2 dejando .48 que representa 480 metros y esto al sumarse con otros calculos de la ruta pueden representar diferencias mayores de 10 kilometros.
como se puede solucionar esto ?
Hola, German. Muy interesante tu pregunta; me daré a la tarea de revisar el código. Por lo pronto, la primera idea que se me ocurre (no será la más brillante) es la de utilizar unidades menores en las medidas de longitud, es decir, si tengo 0.58 km lo paso a 580 metros, lo cual supone convertir la matriz de distancias. Reitero, no es la solución más fina, ya que me demandará revisar el código, pero creería que puede funcionar perfectamente.
Ya revisé la documentación y tanto los registros como las devoluciones de las llamadas de distancias, costos y cualquier otra dimensión solo aceptan números enteros. Tenías razón. Entonces toma relevancia mi solución: Convertir la matriz de distancias previo al VRP para que considere menos unidades de longitud y se pierdan las menores cifras significativas. Modificar el límite que se le da a cada vehículo (por ejemplo distancia máxima recorrida, convertirla a las nuevas unidades). Y, si es el caso, convertir las salidas a las unidades deseadas. Gracias por la retroalimentación. Voy a dejar una nota informativa en el artículo que aborde este particular.