Método gráfico de la programación lineal mediante el uso de Python
Solución gráfica de la PL
Tal como lo mencionamos en el artículo en el que abordamos inicialmente los pasos de resolución gráfica de los modelos de programación lineal; dada la limitación en la cantidad de variables que puede soportar el método gráfico (2 variables), y dada la forma manual de resolución del mismo, este es difícilmente útil en la práctica.
¿Por qué debería aprender a solucionar gráficamente un modelo de PL?
La solución gráfica de los modelos de programación lineal, puede proporcionar una perspectiva que permita un entendimiento más amplio de los métodos generales de resolución (método simplex o solucionadores). Del mismo modo, permite una mayor comprensión de los diversos elementos que componen un modelo de PL (dado su componente visual), siendo especialmente útil en el aprendizaje de diferentes tópicos como pueden ser: tipos de solución, tipos de restricciones y análisis de sensibilidad.
¿Solo puedo solucionar gráficamente un modelo de PL de manera manual?
Si bien hemos reconocido las bondades del aprendizaje de la solución gráfica, razón por la cual su enseñanza perdura en la academia; también hemos de reconocer que la naturaleza manual de sus cálculos y procedimientos gráficos, pueden hacer tedioso su aprendizaje.
Ahora bien, es preciso considerar que gran parte de los programas solucionadores de modelos PL cuentan con algún módulo gráfico interactivo (TORA, WinQSB, por ejemplo), que puede remplazar los procedimientos manuales. Así entonces, existen otras alternativas a los procedimientos y cálculos manuales, que permiten lograr un acercamiento más ágil al método de solución gráfica de PL.
Solución gráfica de programación lineal mediante Python
Ya hemos justificado de manera suficiente la permanencia del método gráfico en los programas de enseñanza de Investigación de Operaciones; sin embargo, es necesario reconocer la posibilidad actual de integrar diversas disciplinas a través de los procesos de aprendizaje que enriquezcan la formación en la materia.
El objetivo de este artículo consiste precisamente en abordar el método gráfico como alternativa de solución de modelos de programación lineal, al tiempo que generamos un código en Python (programación), que nos permita automatizar procedimientos gráficos y cálculos.
El propósito de integrar un lenguaje de programación como lo es Python, consiste en acercar a las personas a la posibilidad de integrar métodos tradicionales de la investigación de operaciones con herramientas tecnológicas vigentes. ¿Por qué Python? Porque es gratuito; está respaldado por los desarrollos de una gran comunidad (casi que existe una línea de código desarrollado para cada requerimiento); sus aplicaciones no se limitan a un área en concreto, y por lo tanto podemos integrar diversos desarrollos a nuestros métodos.
En síntesis, queremos aportar nuevas propuestas en la enseñanza de la investigación de operaciones a través de la programación.
Requisitos técnicos
Los requisitos técnicos varían de acuerdo a si queremos ejecutar los códigos en nuestro equipo, o si queremos utilizar un entorno colaborativo (recomendado).
Requisitos en nuestro equipo
- Tener una versión de Python instalada (preferiblemente una versión posterior a 3.6): Descargar Python 3.8x 64-bit
- Tener una versión de pip (paquetes de instalación) de Python superior a 9.01 (Python 3.4 o superiores vienen con pip incorporado). Esto le permitirá instalar librerías con un comando simple y directo: pip.
- Tener un editor para código, nosotros recomendamos un editor simple, por ejemplo: Sublime Text: Descargar Sublime Text. También puede utilizar un IDE (Entorno de Desarrollo Integrado), como Spyder. Todo dependerá del alcance de su proyecto.
Requisitos en un entorno colaborativo
Podemos utilizar del mismo modo, un entorno virtual. En este caso recomendamos el uso de Colaboratory de Google, un entorno que cuenta con todas las herramientas necesarias para nuestros desarrollos. No tendremos que instalar nada en nuestro equipo, y aprovecharemos la potencia de las máquinas de Google.
Librerías necesarias
Con la instalación de los programas, o el uso de un entorno colaborativo, ya estamos listos para empezar a programar, sin embargo, cada desarrollo, por pequeño que este sea, tiene sus particularidades; y existen herramientas (librerías) que nos facilitan considerablemente nuestros desarrollos, de acuerdo a nuestras necesidades. Para colocarlo en perspectiva, piense en se teléfono celular, tenemos diferentes apps, cada una de ellas nos facilita algunas tareas, de acuerdo a nuestras necesidades; pues bien, así funcionan las librerías en Python.
El desarrollo que queremos lograr requiere de las siguientes librerías:
- Numpy: Numpy es una librería (biblioteca) que contiene un conjunto amplio de soluciones especializadas en cálculos matemáticos de alto nivel. Numpy nos facilita la vida a la hora de trabajar con matrices, vectores, rangos, etc.
Instalar una librería en Python es muy sencillo, de ahí la importancia de contar con pip (paquetes de instalación). Pip nos permite instalar cualquier librería con un comando escrito en la Lista de comandos de Windows (CMD). Recuerde que si utiliza un entorno colaborativo, este incluye gran parte de las librerías necesarias.
Para instalar Numpy tan solo debemos escribir el siguiente comando en la lista de comandos: pip install numpy
Damos ENTER y veremos lo siguiente:
Así de sencillo es instalar una librería en Python.
- Matplotlib: Matplotlib es una librería (biblioteca) completa para crear visualizaciones estáticas, animadas e interactivas en Python. Y bien, si queremos abordar el método gráfico, necesitamos una librería que nos ayude con las gráficas.
Para instalar Matplotlib tan solo debemos escribir el siguiente comando en la lista de comandos: pip install matplotlib
- Shapely: Shapely es una librería (biblioteca) completa que nos permite la manipulación y análisis de objetos geométricos. Nos resultará de mucha ayuda al momento de manipular nuestras gráficas.
Para instalar Shapely tan solo debemos escribir el siguiente comando en la lista de comandos: pip install Shapely
Así de sencillo es instalar librerías en Python. Con estas librerías estamos listos para crear nuestro desarrollo.
El problema
Un autobús que hace el recorrido Cali-Buga, ofrece asientos para fumadores al precio de 10.000 pesos y a no fumadores al precio de 6.000 pesos. Al no fumador se le deja llevar 50 Kg. de peso y al fumador 20 Kg. Si el autobús tiene 90 asientos y admite un equipaje de hasta 3.000 Kg. ¿Cuál ha de ser la oferta de asientos de la compañía para cada tipo de pasajeros, con la finalidad de optimizar el beneficio? Además, debe considerarse que por políticas de la empresa, deben ofrecerse cómo mínimo 10 asientos para pasajeros no fumadores.
Modelamiento mediante programación lineal
Variables
x: Cantidad de asientos reservados a fumadores.
y: Cantidad de asientos reservados a no fumadores.
Restricciones
20x + 50y <= 3000 (Equipaje permitido)
x + y <= 90 (Cantidad de asientos disponibles)
y >= 10 (Política de asientos mínimos para no fumadores)
y >= 0 (No negatividad)
x >= 0 (No negatividad)
Función objetivo
z = 10000x + 6000y (Maximizar)
Método gráfico mediante Python
Paso 1: Importar las librerías
El siguiente fragmento de código importa las librerías necesarias para nuestro desarrollo:
#Librerías necesarias
import matplotlib.pyplot as plt
import numpy as np
from shapely.geometry import LineString
Paso 2: Ecuaciones e intervalos
Para poder graficar las restricciones (paso esencial del método gráfico), es necesario representar las ecuaciones por medio de líneas en nuestra gráfica. Cada restricción estará representada por una línea recta. El paso que antecede trazar una línea recta consiste en la determinación de un mínimo de dos puntos que al unirse la conformen.
Cada punto en el plano cartesiano se encuentra conformado por una coordenada en x y una coordenada en y (en el caso que así definamos llamar a la abscisa y a la ordenada). Recordemos que a partir del modelo algebraico inicial, nuestras restricciones se encuentran representadas por ecuaciones. Así entonces, la tarea consiste en, a partir de una ecuación, obtener un conjunto mínimo de dos coordenadas.
Manualmente este proceso se realiza tabulando, es decir, despejando el valor de una de las variables de la ecuación, a partir de la asignación arbitraria de un valor a la variable restante.
La tarea que tenemos mediante la programación en Python consistirá entonces en automatizar este proceso.
Lo primero que debemos hacer es despejar cada una de las inecuaciones convertidas en ecuaciones del problema, para eso, en nuestro caso, vamos a despejar en función de y:
Por ejemplo, para nuestra primera restricción:
20x + 50y <= 3000 (Inecuación)
20x + 50y = 3000 (Ecuación)
y = (3000 – 20x) / 50 (Despejamos y)
y1 = (3000 – 20x) / 50 (Asignamos un identificador único a y)
Repetimos el procedimiento para nuestra segunda restricción:
x + y <= 90 (Inecuación)
x + y = 90 (Ecuación)
y = 90 – x (Despejamos y)
y2 = 90 – x (Asignamos un identificador único a y)
En el caso de la tercera restricción:
y >= 10 (Inecuación)
y = 10 (Ecuación)
En este caso, dado que la intención es graficar, es fundamental que cada ecuación contenga las dos variables. Dado que en la ecuación original la variable x no hace parte, podemos incluirla multiplicándola por 0. Es decir, para todos los valores que tome x la ecuación permanecerá inalterable.
y = 10 + (0 * x) (Ecuación, y ya se encuentra despejada)
y3 = 10 + (0 * x) (Asignamos un identificador único a y)
En el caso de la cuarta restricción:
y >= 0 (Inecuación)
y = 0 (Ecuación)
En este caso, dado que la intención es graficar, es fundamental que cada ecuación contenga las dos variables. Dado que en la ecuación original la variable x no hace parte, podemos incluirla multiplicándola por 0. Es decir, para todos los valores que tome x la ecuación permanecerá inalterable.
y = 0 * x (Ecuación, y ya se encuentra despejada)
y4 = 0 * x (Asignamos un identificador único a y)
Todas las ecuaciones anteriores tienen algo en común: Se encuentran despejadas para obtener el valor de y a partir de x, de manera que necesitamos alguna función que nos permita asignar diferentes valores a x en un rango dado. Para eso utilizaremos la función np.arange.
x = np.arange(-100, 150, 50)
Esta función permite asignar a x diferentes valores de acuerdo a unos argumentos dados (valor mínimo, valor máximo, intervalo o paso). Es decir que de acuerdo a la anterior línea de código, a la variable x le serán asignados diversos valores desde el valor -100 hasta el valor 150 con intervalos de 50. Así entonces, tomará los siguientes valores:
| x |
| -100 |
| -50 |
| 0 |
| 50 |
| 100 |
| 150 |
Dado que las ecuaciones que pretenden hallar y1, y2, y3 y y4 son dependientes de x, tomarán sus valores respectivos de acuerdo a los resultados de cada ecuación, para cada valor de x:
| x | y1 | y2 | y3 | y4 |
| -100 | 100 | 190 | 10 | 0 |
| -50 | 80 | 140 | 10 | 0 |
| 0 | 60 | 90 | 10 | 0 |
| 50 | 40 | 40 | 10 | 0 |
| 100 | 20 | -10 | 10 | 0 |
| 150 | 0 | -60 | 10 | 0 |
La última de nuestras restricciones (quinta restricción), está dada en función de hallar x a partir y, de manera que efectuamos la misma tarea en un sentido inverso:
x >= 0 (Inecuación)
x = 0 (Ecuación)
En este caso, dado que la intención es graficar, es fundamental que cada ecuación contenga las dos variables. Dado que en la ecuación original la variable y no hace parte, podemos incluirla multiplicándola por 0. Es decir, para todos los valores que tome y la ecuación permanecerá inalterable.
x = 0 * y (Ecuación, x ya se encuentra despejada)
x1 = 0 * y (Asignamos un identificador único a x)
En este caso, ya que requerimos que y tome diversos valores, utilizaremos la función np.arange.
y = np.arange(-100, 150, 50)
Esta función permite asignar a y diferentes valores de acuerdo a unos argumentos dados (valor mínimo, valor máximo, intervalo o paso). Es decir que de acuerdo a la anterior línea de código, a la variable y le serán asignados diversos valores desde el valor -100 hasta el valor 150 con intervalos de 50. Así entonces, tomará los siguientes valores:
| y |
| -100 |
| -50 |
| 0 |
| 50 |
| 100 |
| 150 |
Dada que nuestra quinta restricción pretende hallar x1 a partir de los valores de y, tendríamos lo siguiente:
| y | x1 |
| -100 | 0 |
| -50 | 0 |
| 0 | 0 |
| 50 | 0 |
| 100 | 0 |
| 150 | 0 |
Por último, consideramos la inclusión de la función objetivo, para ello:
10000x + 6000y = 0 (Ecuación)
y = (- 10000x) / 6000 (Despejamos y)
y5 = (- 10000x) / 6000 (Asignamos un identificador único a y)
En este caso, la función que ya asignamos a x (np.arange), nos prestará los valores necesarios para tabular y5.
Lo que hicimos hasta ahora consiste en explicar con alto grado de detalle la función de cada una las líneas del código que utilizaremos en Python. Todo lo anterior queda reducido al siguiente fragmento:
#Ecuaciones e intervalos (Para tabular)
x = np.arange(-100, 150, 50)
y1 = (3000 - (20 * x))/ 50
y2 = 90 - x
y3 = 10 + (0 * x)
y4 = 0 * x
y5 = (-10000 * x) / 6000
y = np.arange(-100, 150, 50)
x1 = 0 * y
Paso 3: Tabular coordenadas e identificar las líneas
En el paso anterior desarrollamos unas líneas de código que representan los cálculos correspondientes a cada una de las ecuaciones del modelo. Si bien con fines prácticos mostramos la forma en que se tabularían los datos, es hasta este paso en que la información se organiza en tablas (propiamente matrices de dos columnas: x y y). La información se organiza a partir de una instancia básica de la librería Numpy, tal como se explicará a continuación:
np.column_stack((x, y1))
Esta instancia tomará los valores del paso 1 y los tabulará en una matriz 2D (dos columnas). En este ejemplo:
| x | y1 |
| -100 | 100 |
| -50 | 80 |
| 0 | 60 |
| 50 | 40 |
| 100 | 20 |
| 150 | 0 |
El siguiente paso consiste en, a partir de una instancia básica de la librería Shapely, generar la línea correspondiente a cada ecuación de acuerdo al tabulado generado, tal como se aprecia a continuación:
LineString(np.column_stack((x, y1)))
LineString es una instancia de la librería Shapely que permite unir cada punto (coordenada), de manera que genera una línea. Ahora bien, cada línea de código deberá corresponder o asociarse a una variable única que nos permitirá identificar cada una de las líneas, por ejemplo:
primera_línea = LineString(np.column_stack((x, y1)))
Realizamos el mismo procedimiento para cada una de las líneas, siendo cuidadosos al momento de asignar las variables asociadas a cada una de las líneas:
#Identificadores para las líneas
primera_linea = LineString(np.column_stack((x, y1)))
segunda_linea = LineString(np.column_stack((x, y2)))
tercera_linea = LineString(np.column_stack((x, y3)))
cuarta_linea = LineString(np.column_stack((x1, y)))
quinta_linea = LineString(np.column_stack((x, y4)))
sexta_linea = LineString(np.column_stack((x, y5)))
Podemos observar como cada conjunto de variables corresponde estrictamente a cada una de las líneas asociadas a cada ecuación en particular.
Paso 4: Graficar las líneas
En este paso vamos a utilizar la librería Matplotlib para graficar nuestras líneas (ecuaciones).
Colores de línea
| Alias | Color |
|---|---|
| b | Azul |
| g | Verde |
| r | Rojo |
| c | Cyan |
| m | Magenta |
| y | Amarillo |
| k | Negro |
| w | Blanco |
Tipos de línea
| Estilo de línea | |
|---|---|
| – | |
| – – | |
| : | |
| : – |
El argumento linewidth determinará el grosor de la línea. Debemos considerar asignar las mismas variables que en el paso anterior.
#Graficando las líneas
plt.plot(x, y1, '-', linewidth=2, color='b')
plt.plot(x, y2, '-', linewidth=2, color='g')
plt.plot(x, y3, '-', linewidth=2, color='r')
plt.plot(x1, y, '-', linewidth=2, color='y')
plt.plot(x, y4, '-', linewidth=2, color='k')
plt.plot(x, z, ':', linewidth=1, color='k')
Ya en este paso tenemos lo suficiente para esbozar nuestras líneas, sin embargo es necesario crear algunas configuraciones generales de nuestra gráfica, y aunque estas líneas de código van al cierre, nos adelantaremos para ir conociendo la evolución parcial de nuestro desarrollo.
#Configuraciones adicionales del gráfico
plt.grid()
plt.xlabel('Asientos para fumadores')
plt.ylabel('Asientos para no fumadores')
plt.title('Método Gráfico')
plt.show()
Estos ajustes permiten asignar los títulos de los ejes, así como el título general del gráfico, así mismo especifica la función que permite que el resultado del código se muestre como imagen.
En este paso queremos ejecutar el código parcial. Nosotros utilizaremos Google Colaboratory, puedes ver la ejecución en nuestro cuaderno: Método Gráfico.
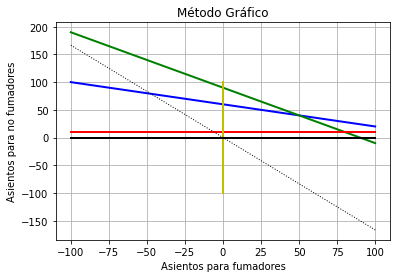
De manera que, de acuerdo al código ejecutado, nuestro programa es capaz de esbozar gráficamente cada una de nuestras ecuaciones sobre el plano cartesiano. Ya que incluso tenemos una representación de la función objetivo (línea punteada), e infiriendo el polígono factible (de acuerdo a la naturaleza de las restricciones: <= o >=), podemos geométricamente establecer cual es el vértice solución.
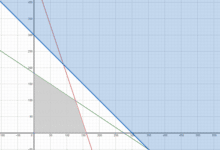
Ahora bien, podemos identificar que en la gráfica se pueden apreciar algunos polígonos, pero: ¿Cuál es nuestro polígono factible? Bien, para eso debemos considerar la naturaleza de las restricciones; en cuyo caso, cada línea trazada dividirá el cuadrante solución en dos semiplanos: uno a cada lado de la línea trazada. Solo una de estas dos mitades satisface cada desigualdad, de manera que debemos considerar si cada restricción es «menor o igual», «mayor o igual», o en su defecto «igual». Por ejemplo:
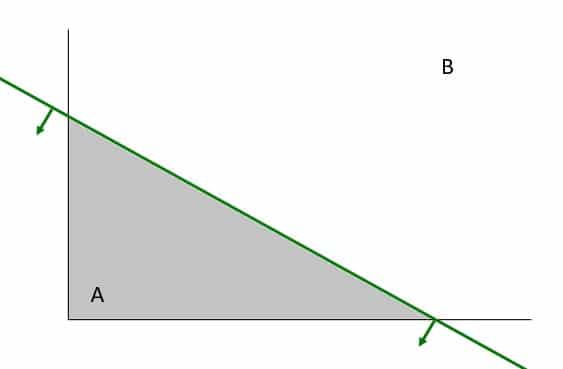
En la anterior gráfica (Figura 5) podemos observar la línea que representa la segunda restricción. Así mismo, podemos observar el concepto de semiplanos: A y B (Uno a cada lado de la línea trazada). Como se trata de una restricción «menor o igual» (líneas hacia abajo y hacia la izquierda); solo la mitad A satisface la desigualdad.
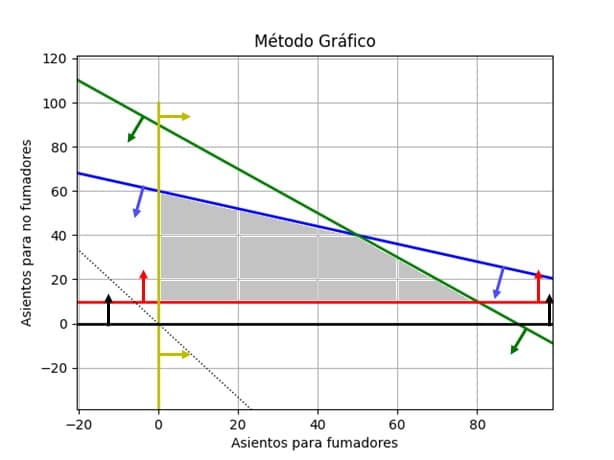
En este caso representamos con flechas el lado, es decir la mitad que divide cada línea trazada, en el cual se encuentran los valores que satisfacen cada restricción. Las restricciones «menores o igual» apuntarán sus flechas hacia abajo y/o a la izquierda; los «mayores o igual» apuntarán sus flechas hacia arriba y/o a la derecha. Así entonces encontramos con suma facilidad nuestro polígono factible (zona gris).
Paso 5: Determinar y graficar las intersecciones
Algunos textos, como por ejemplo Investigación de Operaciones de Taha, consideran que los dos pasos fundamentales de la solución gráfica consisten en: determinar el espacio de soluciones factibles y determinar la solución óptima entre todos los puntos localizados en el espacio de soluciones.
Consideremos que el área gris de la Figura 6 corresponde al polígono o espacio de soluciones factibles. Todos los puntos (coordenadas en x, y) que se encuentran en este espacio, satisfacen al mismo tiempo todas las restricciones del modelo. Los puntos que se encuentra fuera, satisfacen algunas o ninguna de las restricciones.
Ahora bien, la cantidad de puntos dentro del espacio de soluciones factibles es sumamente grande, sin embargo, hemos de recordar que este método se rige bajo criterios de optimización. En nuestro ejemplo, este criterio es: maximizar. Recordemos que en programación lineal, la solución óptima siempre está asociada con un punto de esquina o vértice del polígono factible. Y que estos vértices se generan en cada punto de intersección de dos o más líneas, es decir, en el punto en que se igualan dos o más ecuaciones.
Lo anterior es sumamente importante, ya que para efectos de nuestro desarrollo en Python, podemos utilizar alguna función básica que, dadas las líneas, nos represente las intersecciones. En la práctica, determinar el punto de intersección de dos líneas requiere de la solución de un sistema de ecuaciones de 2 x 2, ya sea por el método de sustitución, igualación, eliminación, etc.
En nuestro caso, vamos a utilizar la función intersection() de Python. Lo que debemos hacer es determinar que intersecciones queremos determinar y graficar. Por ejemplo:
Si queremos determinar la intersección de la línea amarilla (cuarta línea, así la nombramos en el paso anterior) y la línea azul (primera línea), debemos escribir el siguiente código:
primera_interseccion = cuarta_linea.intersection(primera_linea)
Esta línea de código creará una variable llamada primera_interseccion que estará definida por la intersección entre la cuarta línea y la primera línea. El siguiente fragmento creará las intersecciones restantes del polígono solución (consideramos que el orden es importante, así que las creamos de acuerdo a las manecillas del reloj).
#Generando las intersecciones (vértices)
primera_interseccion = cuarta_linea.intersection(primera_linea)
segunda_interseccion = primera_linea.intersection(segunda_linea)
tercera_interseccion = segunda_linea.intersection(tercera_linea)
cuarta_interseccion = tercera_linea.intersection(cuarta_linea)
El espacio de soluciones factibles tienen cuatro intersecciones, de acuerdo al código anterior quedan definidas de acuerdo a los nombres que le asignamos a las variables. Ahora, el paso siguiente consiste en graficar dichas restricciones.
Acá pueden encontrar el listado con los tipos de marcadores (símbolos) que pueden utilizar: marcadores pyplot. Nosotros utilizaremos un marcador en círculo (representado así en el código: «o»).
#Graficando los vértices
plt.plot(*primera_interseccion.xy, 'o', color='k')
plt.plot(*segunda_interseccion.xy, 'o', color='k')
plt.plot(*tercera_interseccion.xy, 'o', color='k')
plt.plot(*cuarta_interseccion.xy, 'o', color='k')
Así entonces, podemos ejecutar nuestro código (Método Gráfico) nuevamente y veremos:
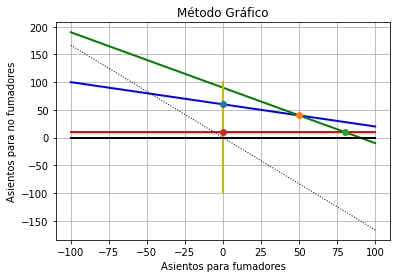
Como podemos observar en la Figura 7, hemos logrado graficar los vértices del polígono factible.
Ahora es cuando debemos preguntarnos: ¿Qué más necesitamos? Pues bien, si bien gráficamente podemos determinar el vértice solución (basta con trasladar paralelamente la línea punteada hasta cada vértice e identificar en cual de ellos la línea no corta el polígono solución); sería importante determinar el valor de las coordenadas en cada uno de los vértices, ya que con ello podemos evaluar la ecuación de la función objetivo para cada punto de esquina.
Lo que necesitamos es el valor numérico de cada punto, y la verdad, ya lo tenemos dentro de nuestras variables; lo que debemos hacer es imprimirlo en la consola de Windows, para eso podemos utilizar el siguiente fragmento:
#Imprimiendo las coordenadas de los vértices en la consola
print('\n COORDENADAS DE LAS INTERSECCIONES')
print('Coordenadas de la primera intersección: {} '.format(primera_interseccion))
print('Coordenadas de la segunda intersección: {} '.format(segunda_interseccion))
print('Coordenadas de la tercera intersección: {} '.format(tercera_interseccion))
print('Coordenadas de la cuarta intersección: {} '.format(cuarta_interseccion))
Bien podíamos utilizar tan solo la función print() en su versión más simple, por ejemplo:
print(primera_interseccion)
Esto serviría para obtener el punto de la primera intersección con sus dos coordenadas (x, y). Sin embargo, hemos utilizado algún texto que identifique con precisión la información que estamos generando. En este caso utilizamos un poco de texto, dentro de las llaves {} el programa introducirá el valor de cada variable. Esta es una cuestión accesoria y de estilo, siéntanse libres de explorar con el código. Ejecutamos (Método Gráfico) y, junto a la imagen, tendremos el siguiente resultado:

De esta manera hemos obtenido los valores de los puntos de cada vértice.
Paso 6: Determinar la solución óptima
Básicamente el objetivo de la solución gráfica se logra en este paso, es decir, hallar la solución óptima en términos de la función objetivo y los valores de las variables de decisión. Con un poco de lógica podemos inferir que en el punto en el que estamos, esta es una cuestión sencilla. Lo único que debemos hacer es, de acuerdo a los valores de cada vértice, evaluar la ecuación de la función objetivo en cada uno de ellos, de manera que podamos determinar cual es el mejor resultado (de acuerdo al criterio de optimización, en este caso: maximizar).
Ya que nos encontramos trabajando en Python, es necesario aclarar que el valor de los vértices obtenidos corresponde a un formato de tipo point (punto), y que básicamente, no es posible operar cada una de las variables (x, y) que contiene sin antes extraerlas. Por esa razón, lo siguiente que debemos hacer es extraer el valor de cada variable contenida en cada punto de manera independiente:
#Identificando los valores de las coordenadas (x, y) de cada vértice
xi1m, yi1m = primera_interseccion.xy
xi2m, yi2m = segunda_interseccion.xy
xi3m, yi3m = tercera_interseccion.xy
xi4m, yi4m = cuarta_interseccion.xy
El anterior código acaba de generar un total de 8 variables, cada una de ellas contendrá la información correspondiente a la proyección de cada eje sobre cada punto, por ejemplo: xi1m contendrá la información correspondiente al valor que tienen el punto de la primera intersección sobre el eje x. Es decir, acabamos de extraer las variables x y y de cada uno de los puntos de intersección.
Sin embargo, ese valor extraído se encuentra en un formato de matriz y contiene más información que la que necesitamos, de hecho por eso le colocamos la letra m, para reconocer que es una matriz. Lo que debemos hacer es cambiar el formato de los valores extraídos. Formas existen muchas, nosotros utilizaremos la siguiente:
#Cambiamos el formato de la variable de matriz a real
xi1 = np.float64(np.array(xi1m))
xi2 = np.float64(np.array(xi2m))
xi3 = np.float64(np.array(xi3m))
xi4 = np.float64(np.array(xi4m))
yi1 = np.float64(np.array(yi1m))
yi2 = np.float64(np.array(yi2m))
yi3 = np.float64(np.array(yi3m))
yi4 = np.float64(np.array(yi4m))
float 64 es un formato que corresponde a números reales, es decir: números que pueden ser positivos o negativos con decimales. En este punto tenemos las variables correspondientes a cada uno de los valores de los vértices en los ejes x y y. Lo siguiente será evaluar la ecuación objetivo en cada uno de los vértices, es decir, en las coordenadas de cada intersección. Por ejemplo:
FOi1 = (xi1 * 10000) + (yi1 * 6000)
Creamos la variable FOi1, es decir: La función objetivo en la intersección 1 (vértice 1). La cual multiplicará los coeficientes de la ecuación objetivo por el valor de la variable xi1 y yi1, es decir, las coordenadas x y y en el vértice 1. En este caso, y ya que conocemos estos valores (los hemos impreso en la consola), generaría el siguiente resultado:
FOi1 = (0 * 10000) + (60 * 6000)
FOi1 = 360000
Lo que equivale a decir que el resultado de la función objetivo en el vértice 1 es igual a 360.000. Así entonces, generamos el fragmento de código de estas ecuaciones y variables, así como las funciones que permitan que estos valores se impriman en la consola:
#Evaluando la función objetivo en cada vértice
FOi1 = (xi1 * 10000) + (yi1 * 6000)
FOi2 = (xi2 * 10000) + (yi2 * 6000)
FOi3 = (xi3 * 10000) + (yi3 * 6000)
FOi4 = (xi4 * 10000) + (yi4 * 6000)
#Imprimiendo las evaluaciones de la FO en cada vértice (Consola)
print('\n EVALUACIÓN DE LA FO EN LOS VÉRTICES')
print('Función objetivo en la intersección 1: {} pesos'.format(FOi1))
print('Función objetivo en la intersección 2: {} pesos'.format(FOi2))
print('Función objetivo en la intersección 3: {} pesos'.format(FOi3))
print('Función objetivo en la intersección 4: {} pesos'.format(FOi4))
Ejecutamos nuestro código (Método Gráfico), y tendremos, además de la gráfica, el siguiente resultado:

A esta altura debemos suponer que estamos muy cerca de lograr que nuestro desarrollo determine, según el criterio de optimización, la solución óptima. Ya que tenemos los valores de la función objetivo en cada uno de los vértices, será cuestión de determinar su valor máximo o mínimo, según se el caso. En nuestro problema, requerimos determinar el valor máximo; para eso utilizamos una función básica de Python:
ZMAX = max(FOi1, FOi2, FOi3, FOi4)
Creamos la variable ZMAX, es decir: La variable que contendrá el valor máximo entre las variables que contienen los valores de la función objetivo en cada vértice. Así entonces obtendremos de una muy sencilla, nuestra solución óptima. El siguiente código creará la variable y la función que permitirá que se imprima dicho resultado en la consola:
#Calculando el mejor resultado (Maximizar)
ZMAX = max(FOi1, FOi2, FOi3, FOi4)
#Imprimiendo la solución óptima en la consola
print('\n SOLUCIÓN ÓPTIMA')
print('Solución óptima: {} pesos'.format(ZMAX))
Ejecutamos nuestro código (Método Gráfico) y tendremos, además de la gráfica, el siguiente resultado:

En este punto nuestro desarrollo permite que obtengamos, además de la gráfica, la solución óptima. ¿Qué más podemos necesitar? Pues bien, necesitamos como mínimo imprimir el valor de las variables de decisión, es decir, el valor de las coordenadas x y y en el vértice donde se encuentra la solución óptima (punto óptimo). En Python pueden existir muchas alternativas para obtener esta información, nosotros utilizaremos el concepto de directorio.
Lo primero que vamos a hacer es organizar la información, es decir, crear un vector que almacene los valores de cada variable (sea x o y) en todos los vértices, por ejemplo:
m = [xi1, xi2, xi3, xi4]
El vector m contendrá los valores (ordenados) de las variables x en cada uno de los vértices, empezando por el vértice 1 y finalizando en el vértice 4. Lo mismo realizamos con las variables y.
n = [yi1, yi2, yi3, yi4]
En este punto, y con la información tal cual como tenemos organizada, podemos realizar un pequeño aporte al gráfico: rellenar nuestro polígono solución. Para eso, utilizamos una función llamada fill, y nuestros vectores recién creados:
plt.fill(m, n, color=’silver’)
Esta función utiliza los vectores m y n para crear un relleno en el gráfico al desplazarse por los puntos de los vectores (coordenadas), en sentido de las manecillas del reloj. Es decir, iniciará en el vértice 1 y finalizará en el vértice 4. Además, hemos especificado que el color de este relleno sea silver:
#Ordenando las coordenadas de los vértices (Las coordenadas x en m y las coordenadas y en n)
m = [xi1, xi2, xi3, xi4]
n = [yi1, yi2, yi3, yi4]
#Graficando el polígono solución a partir de las coordenadas de los vértices
plt.fill(m, n, color='silver')
Ejecutamos nuestro código (Método Gráfico) y tendremos la siguiente gráfica:
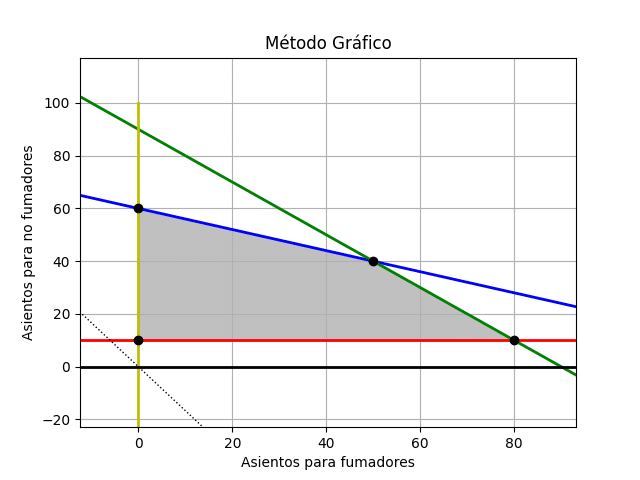
Ahora podemos apreciar el espacio de soluciones factibles desde la gráfica que nos exporta el programa.
Volvamos a nuestro directorio. Lo que vamos a hacer es crear un arreglo con las variables que contienen los resultados de las funciones objetivo (FOi1, FOi2, FOi3 y FOi4), y a cada uno le asignaremos un índice de acuerdo a su orden (ya veremos para qué). Por ejemplo:
dict1 = {0:FOi1, 1:FOi2, 2:FOi3, 3:FOi4}
Así entonces, a cada variable le asignamos un número inicia en 0 y finaliza en 3 (ya veremos para qué). La variable dict hace referencia a nuestro directorio, y dentro de él se encuentra el arreglo con nuestros índices.
Lo siguiente que haremos es extraer el índice, no la variable de este arreglo, de acuerdo al mayor valor de la variable, no del índice. Es decir, una función que evalúe las variables de las funciones objetivo, y en lugar de devolvernos dicho valor, nos traiga el índice que tiene al lado. Nosotros de antemano conocemos que el mayor valor es el de FOi3, por esta razón, la función debe arrojarnos como respuesta el índice 2 (2:FOi3). ¿Por qué no iniciamos desde 1 y sí desde 0? En Python, las posiciones dentro de un arreglo inician desde 0.
La siguiente función nos traerá el índice de acuerdo al mayor valor de la variable:
posicion = max(dict1, key=dict1.get)
Creamos la variable posicion y en ella se almacenará el índice asociado al mayor valor de la variable del arreglo. ¿Y esto para qué nos sirve? Pues bien, recuerdan que tenemos un par de vectores donde se almacenan las variables x y y de cada uno de los vértices (y que hicimos énfasis en ordenarlos). Con la variable posicion podemos acceder a la variable específica dentro de estos vectores, es decir, a la posición en la que se encuentra cada una de las variables asociadas al vértice solución. ¿Podemos plantearlo de una manera más sencilla? Vamos a intentarlo:
Según de la manera ordenada en la que hemos venido trabajando el código, podemos inferir que si la función objetivo solución se encuentra en la variable FOi3 sus coordenadas serán xi3 y y13. Así entonces, si tenemos la posición de la función objetivo dentro de un arreglo (dict1), esa misma posición corresponderá a la de cada variable dentro del vector que la contenga (el vector m contiene las variables x de los vértices, mientras el vector n contiene las variables y de los vértices).
Así entonces, el valor de las coordenadas del vértice solución la obtenemos de la siguiente forma:
XMAX = m[posicion] YMAX = n[posicion]
La variable XMAX tomará el valor de la variable x que se encuentra en el vector m en la posición de la variable posicion. Es decir, corresponderá al valor de la variable x en el vértice solución. Veamos:
#Identificando el índice del vértice de la mejor solución
dict1 = {0:FOi1, 1:FOi2, 2:FOi3, 3:FOi4}
posicion = max(dict1, key=dict1.get)
#Obteniendo las coordenadas del vértice de la mejor solución de acuerdo al índice
XMAX = m[posicion]
YMAX = n[posicion]
#Imprimiendo las coordenadas del vértice de la mejor solución (variables de decisión)
print('\n VARIABLES DE DECISIÓN')
print('Cantidad de asientos a reservar para fumadores: {} '.format(XMAX))
print('Cantidad de asientos a reservar para no fumadores: {} '.format(YMAX))
En el anterior fragmento, bien pudimos utilizar la función print(XMAX) de una manera sencilla. Sin embargo, le dimos un formato que permitiera darle un nombre a las variables de acuerdo al problema (variables de decisión).
Ejecutamos nuestro código y tendremos, además de la gráfica, el siguiente resultado en la consola:

En este punto podemos decir que nuestro código tiene la capacidad de esbozar una solución gráfica del problema de programación lineal. Al mismo tiempo nos permite obtener información básica relevante.
Podemos hacer algunos ajustes accesorios, todos a elección del desarrollador. En este caso, vamos a agregar un par de líneas de código que permitan adicionar al gráfico un par de anotaciones con las coordenadas del vértice solución y el valor la solución óptima. Veamos:
#Generando las anotaciones de las coordenadas y solución óptima en el gráfico
plt.annotate(' X: {0} / Y: {1} (Coordenadas)'.format(XMAX, YMAX), (XMAX, YMAX))
plt.annotate(' Solución óptima: {}'.format(ZMAX), (XMAX, YMAX+3))
Ejecutamos nuestro código (Método Gráfico) y tendremos la siguiente gráfica:
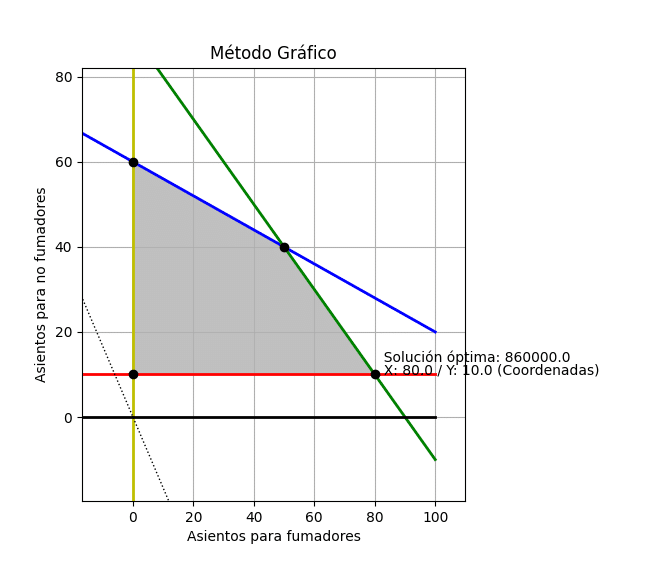
También podemos eliminar las líneas rectas, para ello anteponemos # en la línea que ordena imprimir cada una de las ecuaciones. Ejecutamos (Método Gráfico) y tendremos:
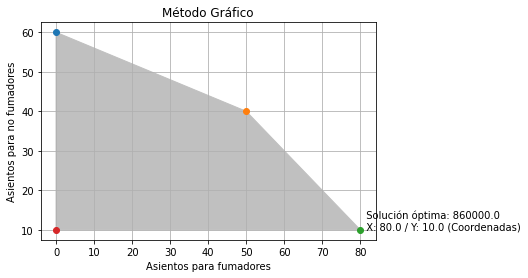
Así entonces, hemos finalizado con la construcción de nuestro código para efectuar una solución gráfica de un modelo de programación lineal. Este puede, con ligeras modificaciones, ajustarse a cualquier problema susceptible de ser solucionado mediante método gráfico.
El código completo de nuestro desarrollo lo presentamos a continuación. También puedes ver el cuaderno de este módulo en nuestro Colaboratory: Método Gráfico.
#Autor: Bryan Salazar López, Ing. M.Sc. (2021)
#Librerías necesarias
import matplotlib.pyplot as plt
import numpy as np
from shapely.geometry import LineString
#Ecuaciones e intervalos (Para tabular)
x = np.arange(-100, 150, 50)
y = np.arange(-100, 150, 50)
y1 = (3000 - (20 * x))/ 50
y2 = 90 - x
y3 = 10 + (0 * x)
x1 = 0 * y
y4 = 0 * x
z = (-10000 * x) / 6000
#Identificadores para las líneas
primera_linea = LineString(np.column_stack((x, y1)))
segunda_linea = LineString(np.column_stack((x, y2)))
tercera_linea = LineString(np.column_stack((x, y3)))
cuarta_linea = LineString(np.column_stack((x1, y)))
quinta_linea = LineString(np.column_stack((x, y4)))
sexta_linea = LineString(np.column_stack((x, z)))
#Graficando las líneas
plt.plot(x, y1, '-', linewidth=2, color='b')
plt.plot(x, y2, '-', linewidth=2, color='g')
plt.plot(x, y3, '-', linewidth=2, color='r')
plt.plot(x1, y, '-', linewidth=2, color='y')
plt.plot(x, y4, '-', linewidth=2, color='k')
plt.plot(x, z, ':', linewidth=1, color='k')
#Generando las intersecciones (vértices)
primera_interseccion = cuarta_linea.intersection(primera_linea)
segunda_interseccion = primera_linea.intersection(segunda_linea)
tercera_interseccion = segunda_linea.intersection(tercera_linea)
cuarta_interseccion = tercera_linea.intersection(cuarta_linea)
#Graficando los vértices
plt.plot(*primera_interseccion.xy, 'o')
plt.plot(*segunda_interseccion.xy, 'o')
plt.plot(*tercera_interseccion.xy, 'o')
plt.plot(*cuarta_interseccion.xy, 'o')
#Imprimiendo las coordenadas de los vértices en la consola
print('\n COORDENADAS DE LAS INTERSECCIONES')
print('Coordenadas de la primera intersección: {} '.format(primera_interseccion))
print('Coordenadas de la segunda intersección: {} '.format(segunda_interseccion))
print('Coordenadas de la tercera intersección: {} '.format(tercera_interseccion))
print('Coordenadas de la cuarta intersección: {} '.format(cuarta_interseccion))
#Identificando los valores de las coordenadas x y y de cada vértice
xi1m, yi1m = primera_interseccion.xy
xi2m, yi2m = segunda_interseccion.xy
xi3m, yi3m = tercera_interseccion.xy
xi4m, yi4m = cuarta_interseccion.xy
#Cambiamos el formato de matriz a float
xi1 = np.float64(np.array(xi1m))
xi2 = np.float64(np.array(xi2m))
xi3 = np.float64(np.array(xi3m))
xi4 = np.float64(np.array(xi4m))
yi1 = np.float64(np.array(yi1m))
yi2 = np.float64(np.array(yi2m))
yi3 = np.float64(np.array(yi3m))
yi4 = np.float64(np.array(yi4m))
#Evaluando la función objetivo en cada vértice
FOi1 = (xi1 * 10000) + (yi1 * 6000)
FOi2 = (xi2 * 10000) + (yi2 * 6000)
FOi3 = (xi3 * 10000) + (yi3 * 6000)
FOi4 = (xi4 * 10000) + (yi4 * 6000)
#Imprimiendo las evaluaciones de la FO en cada vértice (Consola)
print('\n EVALUACIÓN DE LA FO EN LOS VÉRTICES')
print('Función objetivo en la intersección 1: {} pesos'.format(FOi1))
print('Función objetivo en la intersección 2: {} pesos'.format(FOi2))
print('Función objetivo en la intersección 3: {} pesos'.format(FOi3))
print('Función objetivo en la intersección 4: {} pesos'.format(FOi4))
#Calculando el mejor resultado (Maximizar)
ZMAX = max(FOi1, FOi2, FOi3, FOi4)
#Imprimiendo la solución óptima en la consola
print('\n SOLUCIÓN ÓPTIMA')
print('Solución óptima: {} pesos'.format(ZMAX))
#Ordenando las coordenadas de los vértices (Las coordenadas x en m y las coordenadas y en n)
m = [xi1, xi2, xi3, xi4]
n = [yi1, yi2, yi3, yi4]
#Graficando el polígono solución a partir de las coordenadas de los vértices
plt.fill(m, n, color='silver')
#Identificando el índice del vértice de la mejor solución
dict1 = {0:FOi1, 1:FOi2, 2:FOi3, 3:FOi4}
posicion = max(dict1, key=dict1.get)
#Obteniendo las coordenadas del vértice de la mejor solución de acuerdo al índice
XMAX = m[posicion]
YMAX = n[posicion]
#Imprimiendo las coordenadas del vértice de la mejor solución (variables de decisión)
print('\n VARIABLES DE DECISIÓN')
print('Cantidad de asientos a reservar para fumadores: {} '.format(XMAX))
print('Cantidad de asientos a reservar para no fumadores: {} '.format(YMAX))
#Generando las anotaciones de las coordenadas y solución óptima en el gráfico
plt.annotate(' X: {0} / Y: {1} (Coordenadas)'.format(XMAX, YMAX), (XMAX, YMAX))
plt.annotate(' Solución óptima: {}'.format(ZMAX), (XMAX, YMAX+3))
#Configuraciones adicionales del gráfico
plt.grid()
plt.xlabel('Asientos para fumadores')
plt.ylabel('Asientos para no fumadores')
plt.title('Método Gráfico')
plt.show()
En artículos posteriores abordaremos Análisis de sensibilidad en la solución gráfica mediante Python, y evaluaremos la pertinencia de la misma.




De mucha utilidad tu aporte!, muchas gracias :D
¡Hola, Juan!
Un gusto tener autónomos por acá… Siempre bienvenidos, sea por este medio o por cualquier medio de la U.
¿Están viendo IO-1? Pueden escribirme a basalazar@uao.edu.co.