Método Simplex
El Método Simplex es un método analítico de solución de problemas de programación lineal, capaz de resolver modelos más complejos que los resueltos mediante el método gráfico, sin restricción en el número de variables y con una mayor capacidad de análisis de sensibilidad.
El Método Simplex es un método iterativo que permite ir mejorando la solución en cada paso. La razón matemática de esta mejora radica en que el método consiste en caminar del vértice de un poliedro a un vértice vecino de manera que aumente o disminuya (según el contexto de la función objetivo, sea maximizar o minimizar). Dado que el número de vértices que presenta un poliedro solución es finito, en la medida en que se pueda satisfacer el conjunto de restricciones, siempre se hallará como mínimo una solución óptima.
Simplex es considerado como uno de los algoritmos más importantes de la historia, y hoy por hoy sigue siendo la base en la que se fundamentan la mayor parte de solucionadores de modelos de programación lineal.
La importancia de la teoría de matrices en el Método Simplex es fundamental, dado que el algoritmo se basa en dicha teoría para la resolución de sus problemas. De tal manera que veremos previamente, en qué consiste una matriz identidad.
¿Qué es una matriz identidad?
Una matriz puede definirse como una ordenación rectangular de elementos, (o listado finito de elementos), los cuales pueden ser números reales o complejos, dispuestos en forma de filas y de columnas.
La matriz idéntica o identidad es una matriz cuadrada (que posee el mismo número tanto de columnas como de filas) de orden n que tiene todos los elementos diagonales iguales a uno (1) y todos los demás componentes iguales a cero (0), se denomina matriz idéntica o identidad de orden n, y se denota por:
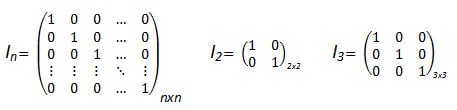
Consideraciones importantes al utilizar el Método Simplex
Variables de holgura y exceso
El Método Simplex trabaja basándose en ecuaciones y las restricciones iniciales que se modelan mediante programación lineal no lo son, para ello hay que convertir estas inecuaciones en ecuaciones utilizando unas variables denominadas de holgura y exceso relacionadas con el recurso al cual hace referencia la restricción y que en el tabulado final representa el «Slack or surplus» al que hacen referencia los famosos programas de resolución de investigación de operaciones, estas variables adquieren un gran valor en el análisis de sensibilidad y juegan un rol fundamental en la creación de la matriz identidad, base del Simplex.
Estas variables suelen estar representadas por la letra «S», se suman (del lado izquierdo de la restricción) si la restricción es de signo «<= » y se restan (del lado izquierdo de la restricción) si la restricción es de signo «>=».
Por ejemplo:


Una consideración importante consiste en que el sistema de restricciones debe ser restrictivo, y esto significa solo una cosa: El lado derecho de las restricciones no puede contener variables, solo un número mayor o igual a 0.
En el caso en que, por ejemplo, tengamos la siguiente restricción:
2X1 + 1X2 + 1X3 + 2X4 <= -24
Procederemos, primero a convertir la desigualdad en igualdad añadiendo una variable de holgura:
2X1 + 1X2 + 1X3 + 2X4 + 1S1 = -24
Segundo, a multiplicar ambos lados de la igualdad por (-1), de tal manera que el lado derecho cumpla con la condición: positivos mayores o iguales a 0.
-2X1 – 1X2 – 1X3 – 2X4 – 1S1 = 24
De esta manera lograríamos estandarizar esta restricción para nuestro algoritmo Simplex.
Variable artificial / Método de la «M»
Una variable artificial es un truco matemático para convertir inecuaciones «>=» en ecuaciones, o cuando aparecen igualdades en el problema original, la característica principal de estas variables es que no deben formar parte de la solución, dado que no representan recursos. El objetivo fundamental de estas variables es la formación de la matriz identidad.
Estas variables se representa por la letra «A», siempre se suman a las restricciones, su coeficiente es M (por esto se le denomina Método de la M grande, donde M significa un número demasiado grande muy poco atractivo para la función objetivo), y el signo en la función objetivo va en contra del sentido de la misma, es decir, en problemas de Maximización su signo es menos (-) y en problemas de Minimización su signo es (+), repetimos con el objetivo de que su valor en la solución sea cero (0).
Variables no negativas
Todas las variables del método Simplex deben cumplir con la condición de no negatividad. Cuando existe alguna variable del modelo que no tiene restricción de no-negatividad, se debe reemplazar por la diferencia de dos variables positivas.
Por lo tanto en el modelo donde aparezca esta variable , se debe cambiar por:
Sea Xi una variable sin restricción de no-negatividad (puede ser mayor, igual o menor que cero), se debe cambiar por:
(Xi(+) – Xi(-)) donde Xi(+) >= 0 y Xi(-) >= 0
Este tipo de variables son poco comúnes, y se utilizan mucho en la programación por metas.
Método Simplex paso a paso
Lo primero que diremos es que la resolución de un problema mediante Método Simplex manual carece de sentido práctico, y solo se utiliza hoy por hoy con fines académicos. Dicho de otro modo, para que el estudiante reconozca el funcionamiento del algoritmo.
Dicho esto, veamos el problema objeto de estudio:
El problema
La empresa el SAMÁN Ltda. Dedicada a la fabricación de muebles, ha ampliado su producción en dos líneas más. Por lo tanto actualmente fabrica mesas, sillas, camas y bibliotecas. Cada mesa requiere de 2 piezas rectangulares de 8 pines, y 2 piezas cuadradas de 4 pines. Cada silla requiere de 1 pieza rectangular de 8 pines y 2 piezas cuadradas de 4 pines, cada cama requiere de 1 pieza rectangular de 8 pines, 1 cuadrada de 4 pines y 2 bases trapezoidales de 2 pines y finalmente cada biblioteca requiere de 2 piezas rectangulares de 8 pines, 2 bases trapezoidales de 2 pines y 4 piezas rectangulares de 2 pines. Cada mesa cuesta producirla $10000 y se vende en $ 30000, cada silla cuesta producirla $ 8000 y se vende en $ 28000, cada cama cuesta producirla $ 20000 y se vende en $ 40000, cada biblioteca cuesta producirla $ 40000 y se vende en $ 60000. El objetivo de la fábrica es maximizar las utilidades.
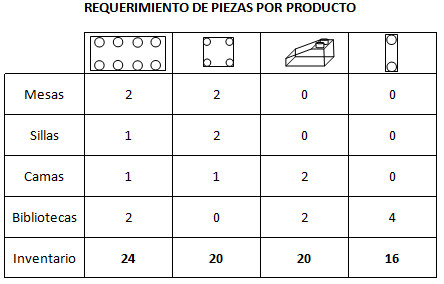
Paso 1: Modelación mediante programación lineal
Variables:
X1 = Cantidad de mesas a producir (unidades)
X2 = Cantidad de sillas a producir (unidades)
X3 = Cantidad de camas a producir (unidades)
X4 = Cantidad de bibliotecas a producir (unidades)
Restricciones:
2X1 + 1X2 + 1X3 + 2X4 <= 24
2X1 + 2X2 + 1X3 <= 20
2X3 + 2X4 <= 20
4X4 <= 16
Función Objetivo:
ZMAX = 20000X1 + 20000X2 + 20000X3 + 20000X4
Paso 2: Estandarizar el modelo
Este paso consiste en cumplir las consideraciones del modelo para que se ajuste al método Simplex:
- Convertir inecuaciones en ecuaciones
- Pasar, de ser necesario, el lado derecho de las restricciones a números positivos.
- Verificar que todas nuestras variables sean de naturaleza no-negativa.
Convertir las inecuaciones en igualdades (Variables de Holgura y Exceso)
En este paso el objetivo es asignar a cada recurso una variable de Holgura, dado que todas las restricciones son «<=».
2X1 + 1X2 + 1X3 + 2X4 + 1S1 + 0S2 + 0S3 + 0S4 = 24
2X1 + 2X2 + 1X3 + 0X4 + 0S1 + 1S2 + 0S3 + 0S4 = 20
0X1 + 0X2 + 2X3 + 2X4 + 0S1 + 0S2 + 1S3 + 0S4 = 20
0X1 + 0X2 + 0X3 + 4X4 + 0S1 + 0S2 + 0S3 + 1S4 = 16
En cuyo caso:
S1 = Cantidad de piezas rectangulares de 8 pines que no se utilizarán (holgura)
S2 = Cantidad de piezas cuadradas de 4 pines que no se utilizarán (holgura)
S3 = Cantidad de bases trapezoidales que no se utilizarán (holgura)
S4 = Cantidad de piezas rectangulares de 2 pines que no se utilizarán (holgura)
De esta manera podemos apreciar una matriz identidad (n = 4), formado por las variables de holgura las cuales solo tienen coeficiente 1 en su respectivo recurso, por ejemplo la variable de holgura «S1» solo tiene coeficiente 1 en la restricción correspondiente al recurso 1.
La función objetivo no sufre variaciones, dado que es un problema de maximización (más adelante veremos qué pasaría si se tratara de un problema de minimización).
ZMAX = 20000X1 + 20000X2 + 20000X3 + 20000X4
Paso 3: Definir la solución básica inicial
El Método Simplex parte de una solución básica inicial para realizar todas sus iteraciones, esta solución básica inicial se forma con las variables cuyo coeficiente es 1 en la matriz identidad.
1S1 = 24
1S2 = 20
1S3 = 20
1S4 = 16
Esto en términos de solución significaría que todos los recursos permanecerían ociosos, y suena lógico, por lo menos suena como un buen punto de partida: inicialmente no se usa ningún recurso.
La tabla simplex
El Método Simplex se hace un poco más sencillo (y esto es mucho decir si estamos abordando una resolución manual), mediante el uso de tabulados simplex.
Cada quien puede agregar o retirar elementos del tabulado, de acuerdo a su utilidad, yo particularmente recomiendo este tabulado base, y luego iré incorporando elementos con un fin pedagógico:

Variable Solución = Todo parte de definir las variables que harán parte de la solución. En esta columna se consigna la solución básica inicial, y a partir de esta en cada iteración se van incluyendo las variables que formarán parte de la solución final.
Solución: (segundo término)= En esta fila se consigna el segundo término de la solución, es decir, el coeficiente de las variables de la columna variable solución, lo más adecuado es que estas se consignen de manera ordenada, tal cual como se escribieron en la definición de restricciones.
Cb = En esta columna se consigna el valor que tiene la variable que se encuentra a su derecha «Variable solución» en la función objetivo.
Cj = Dado que en cada columna se registra una variable (título de la columna), la fila «Cj» hace referencia al coeficiente que tiene cada una de ellas en la función objetivo en la función objetivo.
Zj = En esta fila se consigna la contribución total, es decir la suma de los productos entre el término de cada columna y Cb.
Cj – Zj = En esta fila se realiza la diferencia entre la fila Cj y la fila Zj, su significado es un «Shadow price», es decir, la utilidad que se deja de recibir por cada unidad de la variable correspondiente que no forme parte de la solución. Y representa también el precio dual de las restricciones representadas por las variables de holgura y exceso.
Tabulado con la solución inicial:
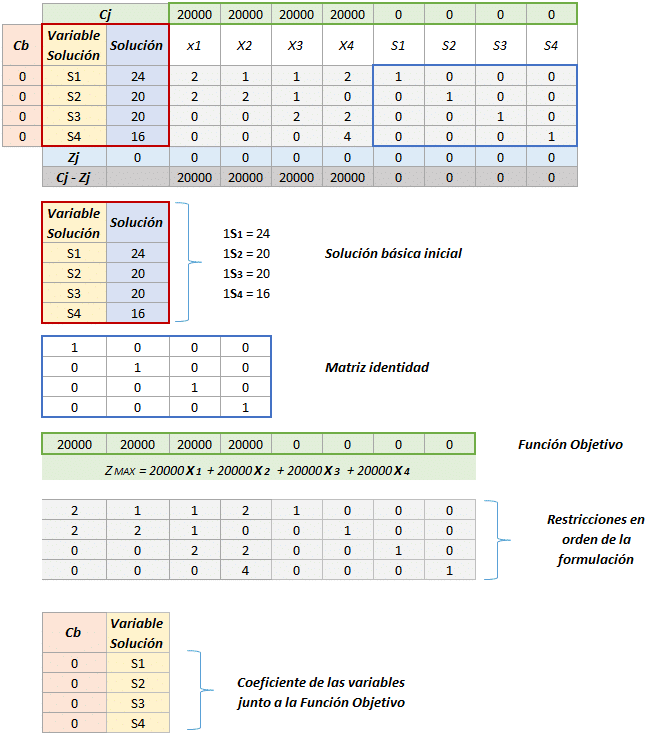
Nota: La base del Simplex es el orden y la organización de la información.
Paso 4: Realizar las iteraciones necesarias
Ya lo dijimos, el Método Simplex es un algoritmo iterativo, y por ende, los criterios para pasar de una iteración a otra son definitivos.
Recordemos algo: El Método Simplex consiste en realizar intentos o recorridos mientras el modelo va de un vértice del poliedro objetivo a otro. Cada recorrido de un vértice a otro estará representato por un tabulado de Simplex o iteración.
¿Qué es lo que pasa en cada iteración? Básicamente una variable entra a la solución inicial, por ende, una variable sale de la solución inicial, y al final de la iteración nos preguntamos si hemos hallado o no la solución óptima.
El procedimiento a seguir es el siguiente:
1. Evaluar que variable entrará y cual saldrá de la solución óptima:

En nuestro caso de ejemplo, todos los Cj – Zj son iguales a 20000, por lo tanto, la decisión debe tomarse de forma arbitraria, es decir, puede elegirse cualquiera como variable de entrada. Elegiremos la variable X4 ¿Por qué? Porque sí, lo estamos haciendo de forma arbitraria para romper el empate.
Dado que X4 es la variable de entrada, los valores que se encuentran en su columna pasarán a ser A. Y B siempre será la columna solución. Veamos:
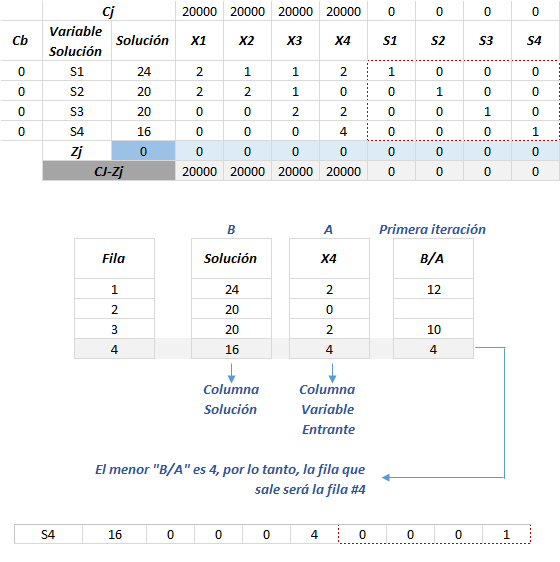
En el caso de la columna temporal A cuando el valor es igual o menor que 0 no se considera para el cálculo de B/A. Por ejemplo, en la fila #2 el valor de A era igual a 0, por lo tanto, no se considera para el cálculo de B/A.
Dado lo anterior, la elección de la fila saliente se da de acuerdo al menor valor de la columna temporal B/A, es decir, entre los valores 20 – 10 – 4. (Tal como observamos en la imagen anterior). Así entonces, la variable que sale será S4.
2. El hecho de que una variable distinta forme parte de las variables solución implica una serie de cambios en el tabulado Simplex, cambios que se explicarán a continuación.
El valor de la intersección entre la columna de la variable que entra y la fila de la variable que sale, se denomina a (minúscula). Veamos en este caso cuál es el a.
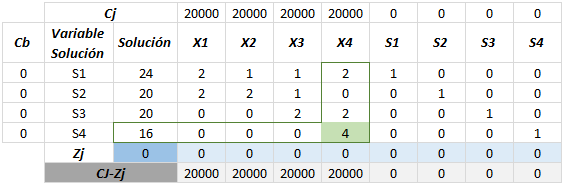
A continuación, todos los valores de la fila de salida se dividen por a.

Como resultado tendremos los valores correspondientes a la nueva fila, en este caso la fila X4.
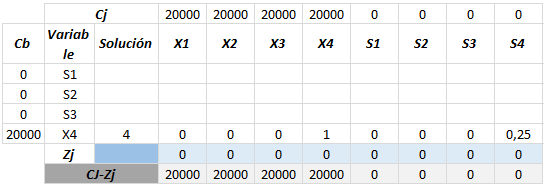
- Lo siguiente corresponde a registrar los nuevos valores de cada fila.
Recordemos que el valor de a depende de la intersección de la columna entrante y cada fila. En este caso vamos a registrar los nuevos valores de la fila # 1, correspondiente a la variable S1. Por lo tanto a será equivalente a 2. Veamos:
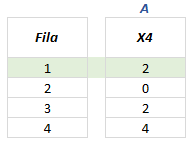
Uno de los pasos más confusos en Simplex es el que se detallará a continuación, sin embargo, es cuestión de prestar suma atención al procedimiento.
La fila de la nueva variable entrante:
![]()
Deberá multiplicarse por el valor de -a (Recordemos que el valor de a para la fila #1 es 2). Es decir, -a es igual a -2. Como resultado tendremos una fila temporal, podemos denominarla – si así lo queremos – por la iteración y la fila, es decir, estamos en la primera iteración, y abordando la fila #1. Su nombre será fila temporal I1-f1 (Esto es algo que me he inventado, espero no complicarlo).

Estos valores, deben sumarse con los valores de la fila 1 que se encontraba en la tabla anterior (S1). Veamos:

Como resultado tendremos los valores correspondientes a la fila1 de la primera iteración, en este caso la fila S1.
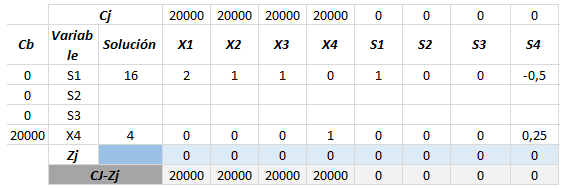
En el caso de la fila 2, recordemos que el valor de a corresponde a 0. Así que los valores pasan tal cual como se encontraban en la tabla anterior.
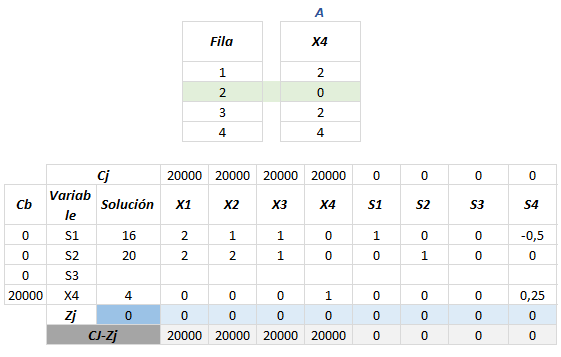
Veamos qué pasa con la tercera fila:

Veamos como queda la tabla:
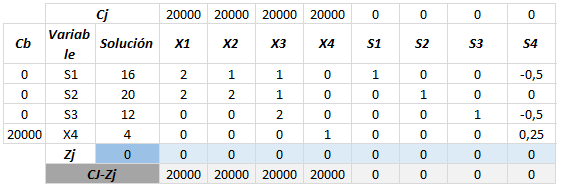
Una vez registrados los valores de toda la tabla, podemos calcular el valor de Zj y Cj – Zj.
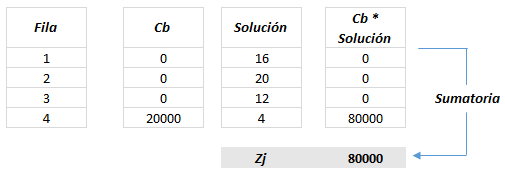
Esta misma operación se efectúa para toda la tabla; es decir, cada columna deberá multiplicarse por Cb. Es recomendable utilizar otra tabla para registrar dichos valores. Al final, deberá sumar los sumar los valores de cada columna y totalizarlos en Zj. A esa tabla le llamaremos: Tabla de productos de Cb:
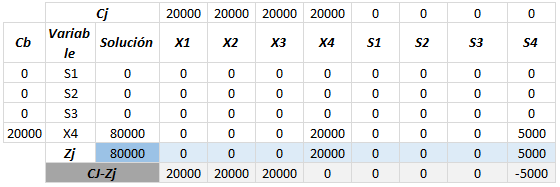
El objetivo de esta tabla anterior es determinar los valores de Zj (Sumatoria de columnas) y Cj-Zj (Diferencia entre la fila Cj y la fila Zj), si ya los tenemos, podemos regresar a nuestra tabla de variables:
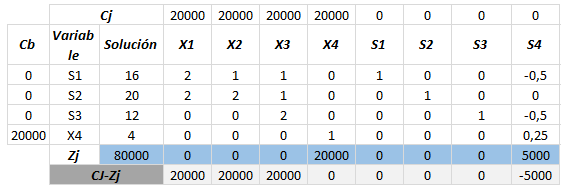
De esta manera se culmina la primera iteración, este paso se repetirá cuantas veces sea necesario y solo se dará por terminado el método según los siguientes criterios.
| Maximizar | Minimizar | |
| Cuando todos los Cj – Zj sean <= 0 | Cuando todos los Cj – Zj sean >= 0 |
- Continuamos con las iteraciones para lo cual tenemos que repetir los pasos anteriores.
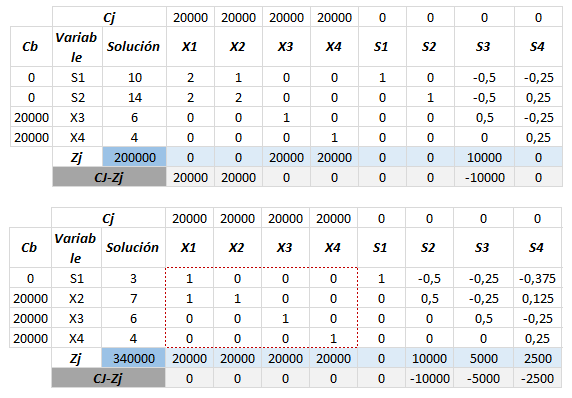
En esta última iteración podemos observar que se cumple con la consigna Cj – Zj <= 0, para ejercicios cuya función objetivo sea «Maximizar», por ende hemos llegado a la respuesta óptima.
X2 = 7
X3 = 6
X4 = 4
S1 = 3 (Cantidad de piezas rectangulares de 8 pines sin utilizar =3)
Función Objetivo: $ 340000
Sin embargo una vez finalizado el Método Simplex se debe observar una matriz identidad en el rectángulo determinado por las variables de decisión (líneas punteadas), el hecho de que en este caso no se muestre la matriz identidad significa que existe una solución óptima alterna.
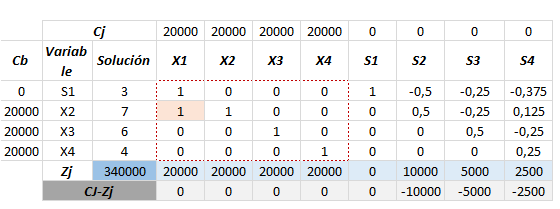
La manera de llegar a la otra solución consiste en alterar el orden en que cada una de las variables entró a la solución básica, recordemos que el proceso fue decidido al azar debido a la igualdad en el Cj – Zj del tabulado inicial. Aquí les presentamos una de las maneras de llegar a la otra solución.
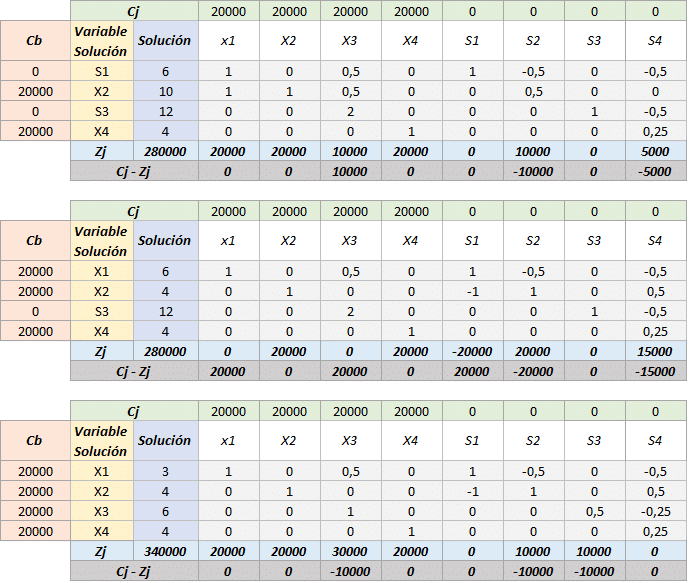
Podemos observar como existe una solución óptima alternativa en la cual la combinación de variables es distinta y existe un menor consumo de recursos, dado que el hecho de que se encuentre la variable «S1» en la solución óptima con un coeficiente de «3» significa que se presenta una holgura de 3 unidades del recurso (pieza rectangular de 8 pines).
X1 = 3 (Cantidad de mesas a producir = 3)
X2 = 4 (Cantidad de sillas a producir = 4)
X3 = 6 (Cantidad de camas a producir = 6)
X4 = 4 (Cantidad de bibliotecas a producir = 4)
Con una utilidad de: $ 340000
Problemas de minimización con el Método Simplex
Para resolver problemas de minimización mediante el algoritmo simplex existen dos procedimientos que se emplean con regularidad.
- El primero, que a mi juicio es el más recomendable se basa en un artificio aplicable al algoritmo fundamentado en la lógica matemática que dicta que «para cualquier función f(x), todo punto que minimice a f(x) maximizará también a – f(x)». Por lo tanto el procedimiento a aplicar es multiplicar por el factor negativo (-1) a toda la función objetivo.
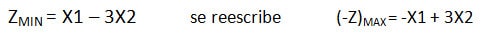
A continuación se resuelve el algoritmo como un problema de maximización.
- El segundo procedimiento, el cual pretende conservar la minimización consiste en aplicar los criterios de decisión que hemos esbozado con anterioridad, en los casos de la variable que entra, que sale y el caso en el que la solución óptima es encontrada. Aquí recordamos los procedimientos según el criterio dado el caso «minimizar».





Estimado BRYN
Soy investigadora cientifica, estoy desarrollando un proyecto de investigacion e innovacion en un prototipo
Me interesa comunicarme con usted, para desarrollar exitosamente mi proyecto.
Hola Marcelle, con gusto. Puedes contactarme en ingenieria@contentlab.co
Buenas tardes, existe un error en la primera iteración entre S1 y X4, que no es 4; es 0 (la columna pivote siempre está conformada por 0 salvo el pivote, que es 1). De ahí que el resto del ejercicio no vaya a presentar el mismo resultado.
Por lo demás, es el mejor desarrollo teórico y práctico de un Simplex que he visto, ya sea en fuentes científicas, manuales prácticos y otros documentos. He de felicitarlo por su labor, explicación y detalle.
Muchas gracias por su labor y entrega.
Hola Jose, agradecemos enormemente tu observación y tus comentarios. De acuerdo, teníamos un error de tipeo, por lo tanto aprovechamos para corregirlo, y consideramos que podíamos mejorar el método de explicación. Espero que el nuevo método utilizado les sea de mucha ayuda. Los invito a seguirnos en nuestras redes y a suscribirse a nuestras notificaciones.
Bryan & Equipo
Buen espfuerzo para presentar un desarrollo Smplex. Lo seguiré estudiando.
Muchas Gracias, y Que tengan muc;hos Exitos
Gracias Eddy por tu comentario. Esperamos que nos visites frecuentemente. No olvides seguirnos en nuestras redes, para que estés al tanto de todo lo nuevo:
Síguenos en Facebook
Síguenos en Linkedin
hola que tal como lo podria implementar bien en excel si me podria ayudar o proporcionarlo para entenderlo de mejor forma
Hola quiero saber porque la función objetivo no sufre variaciones?
La funcion objetivo no sufre variaciones porque tu quieres optimizar un maximo; ventas de la compañia, utilidades;producción en cambio tambien puedes minimizar otras funcione objetivo, costos industriales, insumos en agricultura, remuneraciones. Entonces el metodo simplex es optimizar. Tu como empresario maximizas o minimizas .No puedes variar el objetivo de tu funcion.( Maximizar o Minimizar ) tomas solo uno.
si, mandame mensaje