El modelo de pronóstico de regresión lineal permite hallar el valor esperado de una variable aleatoria a cuando b toma un valor específico. La aplicación de este método implica un supuesto de linealidad cuando la demanda presenta un comportamiento creciente o decreciente, por tal razón, se hace indispensable que previo a la selección de este método exista un análisis de regresión que determine la intensidad de las relaciones entre las variables que componen el modelo.
¿Cuándo utilizar un pronóstico de regresión lineal?
El pronóstico de regresión lineal simple es un modelo óptimo para patrones de demanda con tendencia (creciente o decreciente), es decir, patrones que presenten una relación de linealidad entre la demanda y el tiempo.

Existen medidas de la intensidad de la relación que presentan las variables que son fundamentales para determinar en qué momento es conveniente utilizar regresión lineal.
Análisis de regresión
El objetivo de un análisis de regresión es determinar la relación que existe entre una variable dependiente y una o más variables independientes. Para poder realizar esta relación, se debe postular una relación funcional entre las variables.
Cuando se trata de una variable independiente, la forma funcional que más se utiliza en la práctica es la relación lineal. El análisis de regresión entonces determina la intensidad entre las variables a través de coeficientes de correlación y determinación.
Coeficiente de correlación [r]

El cálculo del coeficiente de correlación se efectúa de la siguiente manera:

Fórmulas


Donde:

Ejemplo de aplicación de un pronóstico de Regresión lineal Simple
La juguetería Gaby desea estimar mediante regresión lineal simple las ventas para el mes de Julio de su nuevo carrito infantil «Mate». La información del comportamiento de las ventas de todos sus almacenes de cadena se presenta en el siguiente tabulado.
| Mes | Periodo | Ventas |
| Enero | 1 | 7000 |
| Febrero | 2 | 9000 |
| Marzo | 3 | 5000 |
| Abril | 4 | 11000 |
| Mayo | 5 | 10000 |
| Junio | 6 | 13000 |
El primer paso para encontrar el pronóstico del mes 7 consiste en hallar la pendiente, para ello efectuamos los siguientes cálculos:







Parece complejo, sin embargo, esta serie de cálculos se aprecian sencillos por medio de un tabulado.
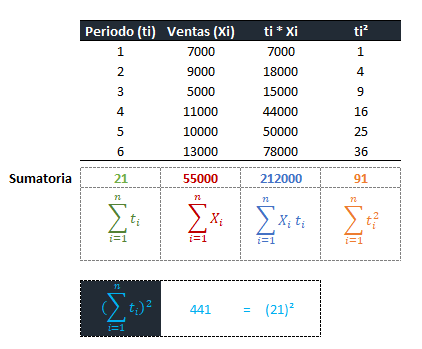
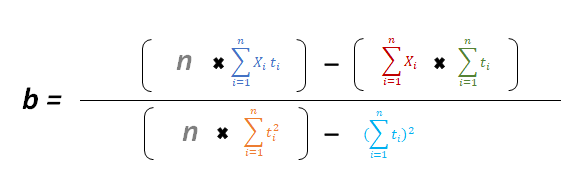
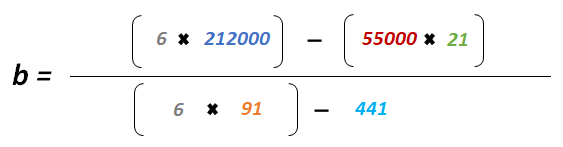


Veámoslo de acuerdo a nuestra explicación con colores:
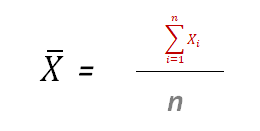
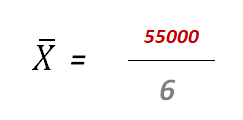
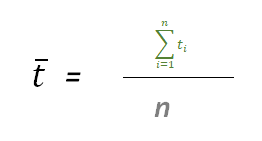
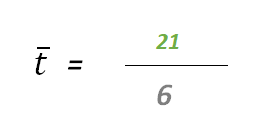
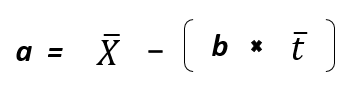

Podemos así determinar que el pronóstico de ventas para el período 7 es equivalente a 13067 unidades.

Calcula tu pronóstico regresión lineal
El siguiente formato ha sido desarrollado por nuestro equipo para efectuar tu pronóstico de una forma sencilla, de esta forma obtendrás de una manera sencilla el pronóstico mediante regresión lineal.





en e lgrafico la recta cruza el eje Y mas o menos en 6600 y debe ser en 5266. Habria un error.
Hola Carlos, un saludo. Al tratarse de un gráfico que pretende esbozar una comparación entre los valores reales (ventas) y la línea de regresión (pronóstico), si puedes observar, el eje X inicia en el período 1, es decir, omitimos el período 0, punto en el cuál la línea de regresión tendría intersección con el eje Y en el valor de 5.266, tal como lo sugieres. Gracias por tu observación, espero haber resuelto tu inquietud, nos leemos por acá.
Me podrías explicar de dónde salió este resultado, que se multiplicó o dividió para este resultado b=1114.28
Hola estimado
Tengo el siguiente problema:
En la teoría económica, se asume una relación de causalidad del ingreso (𝑌) sobre el gasto (𝐺); más aún, el impacto de un incremento en el ingreso es en un periodo posterior. Si 𝑡 representa el paso del tiempo y se asume una relación de causalidad lineal, de los siguientes modelos, el que mejor representa esta proposición es:
a) 𝑮𝒕 = 𝝁 + 𝖰𝒀𝒕 +∈𝒕
b) 𝑮𝒕 = 𝝁 + 𝖰𝒀𝒕 + 𝒕 + 𝝐𝒕
c) 𝑮𝒕 = 𝝁 + 𝖰𝒀𝒕−𝟏 + 𝜺𝒕