Programación lineal en Tora
El software TORA de optimización es un programa basado en Windows®, que tiene por objeto usarse con muchas de las técnicas presentadas en el libro Investigación de Operaciones de TAHA . TORA es una aplicación muy simple, con una interfaz gráfica de baja calidad. Una de las ventajas de TORA es que puede utilizarse en procesadores de 32 y 64 bits, hoy por hoy su principal desventaja es que deberá ajustarse la configuración de pantalla para adecuarse a sus ajustes de presentación de 800 x 600 y 1024 x 768 pixeles. Se recomienda el segundo ajuste, porque produce una distribución más proporcionada de la pantalla.
Solución de un problema de programación lineal con Tora
Al igual que para cualquier otro método de resolución, el primer paso para resolver un problema de programación lineal (PL), consiste en el modelamiento matemático, y es en esta fase en la que el profesional de Ingeniería Industrial debe desarrollar su mayor habilidad y destreza. Los pasos para resolver un problema de PL se encuentran en el módulo de programación lineal.
El problema
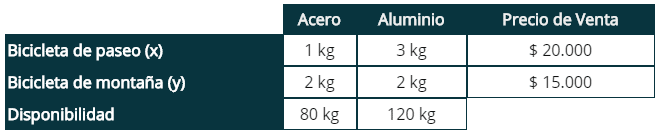
Un herrero con 80 Kg. de acero y 120 Kg. de aluminio quiere hacer bicicletas de paseo y de montaña que quiere vender, respectivamente a 20.000 y 15.000 pesos cada una para sacar el máximo beneficio. Para la de paseo empleará 1 Kg. De acero y 3 Kg. de aluminio, y para la de montaña 2 Kg. de ambos metales. ¿Cuántas bicicletas de paseo y de montaña deberá fabricar para maximizar las utilidades?
El modelo matemático
Declaración de variables
x = Cantidad de bicicletas de paseo a producir
y = Cantidad de bicicletas de montaña a producir
Restricciones de capacidad
Aluminio:
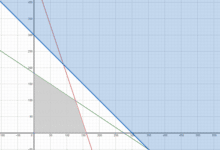
x + 2y <= 80
Acero:
3x + 2y <= 120
Función Objetivo
Zmax = 20000x + 15000y
Ingresando los datos a TORA
Una vez iniciado TORA nos mostrará su menú principal de opciones, en él seleccionamos la opción Linear Programming.

Una vez seleccionada la opción de programación lineal, nos mostrará un menú desde el cual podemos elegir si iniciar un nuevo modelo, o abrir un archivo existente; además de seleccionar el formato de ingreso de datos, en el cual recomendamos el formato decimal:

El siguiente paso consiste en completar la información solicitada en la nueva ventana, correspondiente al nombre del problema, la cantidad de variables y restricciones:

Una vez consignada la información anterior, y luego de teclear ENTER, nos mostrará la siguiente interfaz, en la cual debemos consignar la información del modelo, se trata de un formato tipo matricial muy similar al utilizado por WinQSB:

Una vez completa la información de la matriz, procedemos a resolver el modelo, presionando el botón SOLVE.
Una vez hagamos esto nos mostrará un menú en el que podemos modificar el formato numérico de la solución. Luego de esto, nos mostrará un menú emergente en el que podemos elegir el tipo de solución que queremos visualizar, se encuentra la solución gráfica y la algebraica, elegimos la algebraica en este caso y seleccionamos que se nos muestre el tabulado final:

En el tabulado solución podemos observar como la función objetivo toma el mismo valor obtenido con los programas de solución de Solver y WinQSB. A partir de este tabulado podemos efectuar un análisis de sensibilidad teniendo en cuenta que:

Objective Value: Nos muestra el resultado de nuestra función objetivo, en este caso la solución óptima tiene una función objetivo (utilidad) de $ 850.000.
Value: El valor que toman las variables de decisión.
Obj Val Contrib: Es la contribución unitaria de las variables de decisión en la función objetivo.
Slack-/Surplus+: Cuando la restricción en cuestión tiene el operador <=, corresponde a una holgura, es decir, se puede interpretar como el recurso no utilizado. Cuando la restricción en cuestión tiene el operador >=, corresponde a un exceso, es decir, se puede interpretar como el recurso utilizado por encima de la restricción de mínimo uso.
Min and Max Obj Coeff: Para un coeficiente de la función objetivo en particular. Este es el rango en que la base actual de la solución sigue siendo la misma.
Dual price: Llamado en WinQSB como Shadow Price, y en Solver como Multiplicador de Lagrange, corresponde al cambio marginal de la función objetivo cuando el valor del lado derecho de la restricción aumenta en una unidad.
En nuestro ejemplo sería así: por cada kg de acero adicional que tengamos disponible, la función objetivo aumentará en $1250.




Hola, gracias por tu información, me es muy útil
hice el mismo ejercicio en solver y me resultó diferente, siendo 26.7 y 24 los valores y 893333 la solución optima
así mismo otra página llamada php, con el optimo 600000 x1 0 y x2 40. sabes cual puede ser la razón?
Hola Constanza, precisamente este ejercicio lo resolvimos mediante Solver y WinQSB en este mismo sitio, obteniendo el mismo resultado. Te recomendaría revisar el artículo: https://ingenieriaindustrialonline.com/investigacion-de-operaciones/programacion-lineal-en-solver/ . Quizá sea un problema de modelación.