Programación lineal en Solver
Solver es una herramienta que forma parte de una serie de comandos, a veces denominados de «análisis Y si». Con Solver, puede buscarse el valor óptimo para una fórmula de celda, denominada celda objetivo, en una hoja de cálculo.
Solver funciona en un grupo de celdas que estén relacionadas, directa o indirectamente, con la fórmula de la celda objetivo. Solver ajusta los valores en las celdas cambiantes que se especifiquen, denominadas celdas ajustables, para generar el resultado especificado en la fórmula de la celda objetivo.
Pueden aplicarse restricciones para restringir los valores que puede utilizar Solver en el modelo y las restricciones pueden hacer referencia a otras celdas a las que afecte la fórmula de la celda objetivo, lo cual lo constituyen en una herramienta adecuada para solucionar problemas de programación lineal, y programación lineal entera.
Algoritmos y métodos utilizados por Solver
La herramienta Microsoft Excel Solver utiliza el código de optimización no lineal (GRG2) desarrollado por la Universidad Leon Lasdon de Austin (Texas) y la Universidad Allan Waren (Cleveland).
Los problemas lineales y enteros utilizan el Método Simplex con límites en las variables y el método de ramificación y límite (método de branch and bound), implantado por John Watson y Dan Fylstra de Frontline Systems, Inc. El método de branch and bound corresponde al mismo método utilizado por WinQSB para la solución de problemas de programación lineal entera y/o que utilicen variables binarias.
¿Cómo habilitar el complemento Solver de Excel?
Microsoft Office 2010
El primer paso consiste en dirigirse a la pestaña Archivo, dirigirse a la opción Ayuda y seleccionar la opción Opciones:

Luego, se abrirá una ventana emergente de Opciones de Excel, en ella vamos a la opción Complementos (ubicada en la barra lateral izquierda). Ya en complementos, nos dirigimos a la opción Administrar: Complementos de Excel y damos clic en botón Ir:

Luego se abrirá una pequeña ventana emergente, en ella se podrán observar varios complementos junto con una casilla de verificación cada uno. Activamos la casilla de verificación de Solver y damos clic en Aceptar:

Una vez se ha habilitado el complemento, Solver se ubicará en la pestaña de Datos.
Solución de un problema de programación lineal mediante Solver
Al igual que para cualquier otro método de resolución, el primer paso para resolver un problema de programación lineal (PL) consiste en el modelamiento matemático, y es en esta fase en la que el profesional de Ingeniería Industrial debe desarrollar su mayor habilidad y destreza. Los pasos para resolver un problema de PL se encuentran en el módulo de programación lineal. Sin embargo, dada la interfaz de Excel, el modelamiento se hace más simple, siempre y cuando nos caractericemos por organizar muy bien la información.
El problema
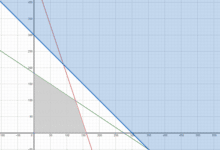
Un herrero con 80 Kg. de acero y 120 Kg. de aluminio quiere hacer bicicletas de paseo y de montaña que quiere vender, respectivamente a 20.000 y 15.000 pesos cada una para sacar el máximo beneficio. Para la de paseo empleará 1 Kg. De acero y 3 Kg. de aluminio, y para la de montaña 2 Kg. de ambos metales. ¿Cuántas bicicletas de paseo y de montaña deberá fabricar para maximizar las utilidades?
El modelo matemático

Declaración de variables
x = Cantidad de bicicletas de paseo a producir
y = Cantidad de bicicletas de montaña a producir
Restricciones de capacidad
Aluminio:
x + 2y <= 80
Acero:
3x + 2y <= 120
Función Objetivo
Zmax = 20000x + 15000y
Ingresando los datos a Excel
Tal cómo se mencionó, la importancia de una correcta organización de la información es vital, proponemos la siguiente plantilla para ingresar los datos de nuestro problema:

El siguiente paso corresponde a registrar la información en la plantilla, de acuerdo a los datos que tenemos en el problema:

El siguiente paso consiste en formular la plantilla, para ello debemos considerar ¿qué pasaría si cambiaran las variables de decisión? Pues, en caso tal de que las variables sufrieran cambios se alteraría la contribución total, y el inventario de recursos. Por ello, debemos formular en consecuencia:

Ahora que ya tenemos nuestra plantilla formulada, el siguiente paso consiste en utilizar Solver para resolver el modelo, para ello, vamos a la pestaña Datos (En cualquier versión de Office), y seleccionamos el complemento Solver:

Una vez iniciemos Solver se abrirá una ventana emergente llamada Parámetros de Solver, en ella como primera medida seleccionaremos nuestra celda objetivo (Contribución Total) y seleccionaremos el criterio Maximizar:

El siguiente paso, es indicarle a Solver que debe alcanzar el máximo valor para la celda objetivo mediante la variación de las siguientes celdas (Cambiando las celdas), es decir, le indicaremos cuales son las variables de decisión:



El siguiente paso consiste en asignarle las restricciones a las que el modelo está sujeto, las cuales son restricciones de disponibilidad de recursos:


Lo que nos muestra la imagen anterior es la forma de indicarle la restricción a Solver, para que el inventario usado sea menor o igual al inventario disponible. De igual forma debe hacerse para el recurso de Aluminio.

La siguiente restricción es la de no negatividad, es decir, que las variables de decisión no puedan tomar valores menores que cero.

Si quisiéramos resolver el modelo tal cual como está pudiésemos hacerlo, y obtendríamos quizá una respuesta que distaría de su aplicación práctica, dado que es probable que la respuesta nos de variables continuas, y en la práctica vender 0,6 bicicletas es un poco complicado. Por tal razón, agregaremos una restricción que hace que el ejercicio se resuelva mediante programación lineal entera, indicando que las variables de decisión deban ser enteras:

Hecho esto, damos clic en Aceptar y en Resolver… Podemos observar como las variables de decisión, las restricciones (inventario usado) y la contribución total (celda objetivo) han tomado valores, estos son los valores óptimos según el modelo formulado. Ahora nos aparecerá un cuadro de diálogo que nos preguntará si deseamos utilizar la solución de Solver y unos informes que debemos seleccionar para obtener una tabla resumen de la respuesta y un análisis de sensibilidad que se insertarán como hojas al archivo de Excel:

El informe de sensibilidad arrojado por Solver es mucho más básico que el que nos puede proporcionar WinQSB, sin embargo destacamos la información referente al «Multiplicador de Lagrange» que corresponde al «Shadow Price de WinQSB» conocido como el precio sombra, es decir, el cambio marginal de la función objetivo cuando el valor del lado derecho de la restricción aumenta en una unidad, en este caso, por cada kg de Acero adicional que dispongamos, la función objetivo aumentaría en $ 1250.

Este mismo ejercicio fue resuelto con WinQSB y TORA arrojando iguales resultados, el archivo de Excel utilizado para esta demostración se adjuntará a continuación para su descarga:
Programación lineal con SOLVER¿Cómo resolver ejercicios de programación lineal en Solver – Video?




Como se formula en esa plantilla