El contexto en el que se aplica el modelo de transporte es amplio y puede generar soluciones relacionadas con el área de operaciones, inventario y asignación de elementos.
El procedimiento de resolución de un modelo de transporte se puede llevar a cabo mediante programación lineal común, sin embargo su estructura permite la creación de múltiples alternativas de solución tales como los modelos de asignación, o los métodos de flujos de red. También es posible emplear los heurísticos más populares como Vogel, Esquina Noroeste o Mínimos Costos.
Los problemas de transporte o distribución son uno de los más aplicados en la economía actual, dejando, como es de prever, múltiples casos de éxito a escala global que estimulan la aprehensión de los mismos.
Problema de transporte mediante programación lineal
Como se mencionó anteriormente, la programación lineal puede ser utilizada para la resolución de modelos de transporte, aunque no sea sensato resolver los modelos mediante el Método Simplex, si puede ser de gran utilidad la fase de modelización, ya que la programación carece de la practicidad de los métodos de asignación, pero puede ser de gran importancia dependiendo de la complejidad de las restricciones adicionales que puede presentar un problema particular.
El problema
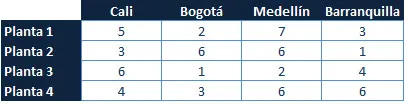
Una empresa energética colombiana dispone de cuatro plantas de generación para satisfacer la demanda diaria eléctrica en cuatro ciudades, Cali, Bogotá, Medellín y Barranquilla. Las plantas 1,2,3 y 4 pueden satisfacer 80, 30, 60 y 45 millones de KW al día respectivamente. Las necesidades de las ciudades de Cali, Bogotá, Medellín y Barranquilla son de 70, 40, 70 y 35 millones de Kw al día respectivamente. Los costos asociados al envío de suministro energético por cada millón de KW entre cada planta y cada ciudad son los registrados en la siguiente tabla.
Solución mediante programación lineal
El modelo básico de transporte es el modelo en el cual la cantidad ofertada es igual a la cantidad demandada, como es el caso de este ejercicio, sin embargo trasladar esta suposición a la realidad es casi imposible por lo cual hace falta crear orígenes y/o destinos ficticios con el excedente de oferta y/o demanda (es sugerible que se haga con la demanda).
Como ya lo hemos planteado en módulos anteriores el primer paso corresponde a la definición de las variables, regularmente se le denomina a las variables de manera algebraica Xi,j donde i simboliza a la fuente y j simboliza al destino. En este caso i define el conjunto {Planta 1, Planta 2, Planta 3 y Planta 4}, y j define el conjunto {Cali, Bogotá, Medellín y Barranquilla}. Sin embargo es práctico renombrar cada fuente y destino por un número respectivo, por ende la variable X1,2 corresponde a la cantidad de millones de KW enviados diariamente de la Planta 1 a la ciudad de Bogotá.
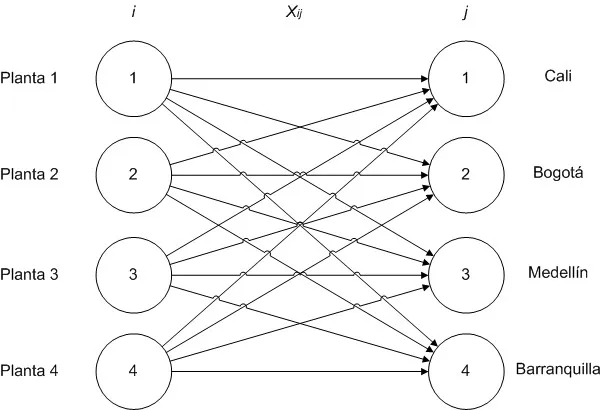
El segundo paso corresponde a la formulación de las restricciones de oferta y demanda, cuya cantidad se encuentra determinada por el factor entre fuentes y destinos, en este caso 16 restricciones.
Restricciones de oferta o disponibilidad, las cuales son de signo ≤:
X1,1 + X1,2 + X1,3 + X1,4 ≤ 80
X2,1 + X2,2 + X2,3 + X2,4 ≤ 30
X3,1 + X3,2 + X3,3 + X3,4 ≤ 60
X4,1 + X4,2 + X4,3 + X4,4 ≤ 45
Restricciones de demanda, las cuales son de signo ≥:
X1,1 + X2,1 + X3,1 + X4,1 ≥ 70
X1,2 + X2,2 + X3,2 + X4,2 ≥ 40
X1,3 + X2,3 + X3,3 + X4,3 ≥ 70
X1,4 + X2,4 + X3,4 + X4,4 ≥ 35
Luego se procede a formular la función objetivo, en la cual se relaciona el costo correspondiente a cada ruta.
ZMIN = 5X1,1 + 2X1,2 + 7X1,3 + 3X1,4 + 3X2,1 + 6X2,2 + 6X2,3 + 1X2,4 + 6X3,1 + 1X3,2 + 2X3,3 + 4X3,4 + 4X4,1 + 3X4,2 + 6X4,3 + 6X4,4
Luego se puede proceder al uso de la herramienta WinQSB para resolver el modelo realizado, aquí están los resultados.
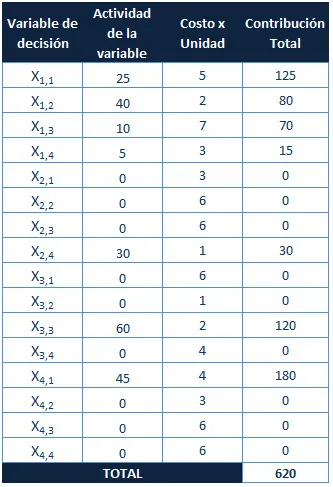
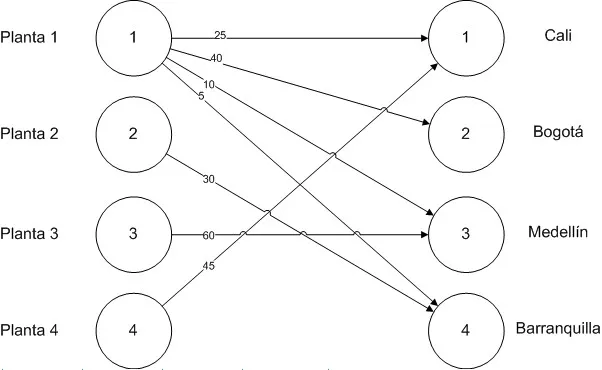
Este problema presenta una solución óptima alternativa, aquí los resultados.
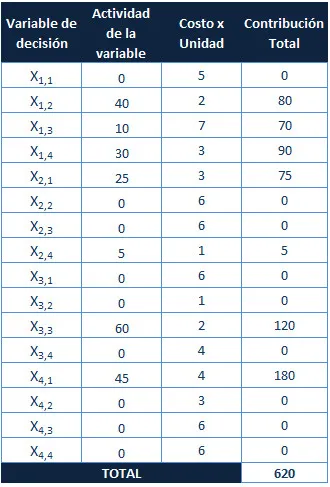
Red solución:
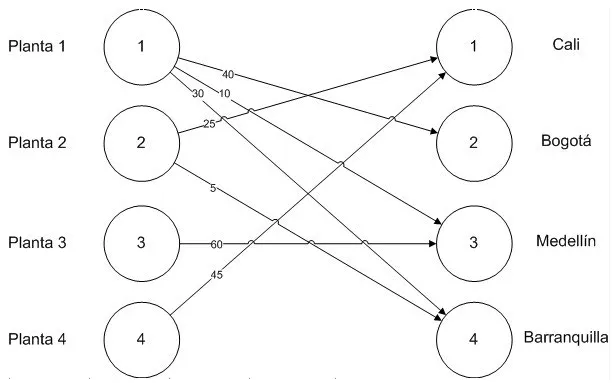
Los análisis de dualidad y sensibilidad en los modelos de transporte resultan ser bastante interesantes, pues pueden llegar a determinar aumentos de capacidad en las fuentes si el precio sombra de las rutas en relación a ellas lo justifica.




HOLA
Quiero saber si hay una diferencia o mas entre la programación lineal y un problema de transporte?
Hola, muchas gracias por tu articulo, muy útil. Pero que sucede en los casos en los cuales puede haber un exceso de oferta en las plantas y se pueda almacenar producción en las plantas con cierto costo de almacenamiento. Como calculo lo optimo a enviar? Saludos
Estimado Buenas Tardes
Junto con saludar quisiera consultar, por que no es sensato resolver un problema de transporte con método simplex, entendí que a nivel de complemento sí en una etapa posterior, podría entrar en detalles de ¿por qué? ¿desventajas de resolverlo en primera instnacia?
quedo atento a sus comentarios.
Hola Axel, recibe un cordial saludo.
Uno de los principales argumentos, consiste en que Simplex no está concebido para resolver problemas mixtos o enteros; y en la práctica, es muy común que un problema de transporte, requiera de la consideración de este tipo de variables.
Por otro lado, en la actualidad, no solo en Investigación de Operaciones, sino en muchos otros campos, como en la ciencia de datos, en procesos de compra y venta, en el marketing mismo, la principal consideración viene de la mano del volumen de datos, el volumen de variables, y la complejidad de las relaciones entre estos. Dicho esto, la automatización en los procesos de captura y procesamiento de datos, la velocidad de los solucionadores, entre otros, juegan un papel fundamental. El problema de transporte, de transbordo y los problemas de enrutamiento, cuando tienen una connotación práctica, requieren de métodos de resolución robustos, de solucionadores potentes, y de mecanismos de automatización de datos. Una buena mezcla de esto puede ser: Un modelamiento mediante programación basada en restricciones + Un solucionador que utilice branch & bound + un lenguaje de programación que permita automatizar captura de datos como Python.
Puedes ver un ejemplo de esto en: https://ingenieriaindustrialonline.com/investigacion-de-operaciones/programacion-lineal-mixta-con-google-or-tools/